题目内容
5. 用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )
用轻绳拴着一质量为m、带正电的小球在竖直面内绕O点做圆周运动,竖直面内加有竖直向下的匀强电场,电场强度为E,如图甲所示,不计一切阻力,小球运动到最高点时的动能Ek与绳中张力F间的关系如图乙所示,当地的重力加速度为g,由图可推知( )| A. | 轻绳的长度为$\frac{2a}{b}$ | B. | 小球所带电荷量为$\frac{b+mg}{E}$ | ||
| C. | 小球在最高点的最小速度为$\sqrt{\frac{2a}{m}}$ | D. | 小球在最高点的最小速度为$\sqrt{\frac{5a}{m}}$ |
分析 小球在竖直面内做圆周运动,到最高点时由绳对小球的拉力、重力和电场力的合力提供向心力,根据图象、应用向心力公式、牛顿第二定律分析答题.写出EK-F的表达式,找到斜率和截距代表的意义,即可解题.
解答 解:A、在最高点时,绳对小球的拉力、重力和电场力的合力提供向心力,则得:F+mg+Eq=m$\frac{{v}^{2}}{L}$,即$\frac{1}{2}$mv2•($\frac{2}{L}$)=F+mg+Eq,由于EK=$\frac{1}{2}m{v}^{2}$,故EK=$\frac{L}{2}$F+$\frac{L}{2}$(mg+Eq),由图象可知,图象斜率k=$\frac{a}{b}$=$\frac{L}{2}$,即L=$\frac{2a}{b}$,故A正确;
B、当F=0时,由mg+Eq=m$\frac{{v}^{2}}{L}$,$\frac{1}{2}m{v}^{2}$=a,解得,q=$\frac{b-mg}{E}$,故B错误;
C、当F=0时,重力和电场力提供向心力,此时为最小速度,$\frac{1}{2}m{v}^{2}$=a,解得v=$\sqrt{\frac{2a}{m}}$,故C正确,D错误;
故选:AC
点评 本题主要考查了圆周运动向心力公式和机械能守恒定律的综合应用,关键要正确分析小球圆周运动的向心力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
4. 如图所示,在水平转台上放一个质量M=2.0kg的木块,它与台面间的最大静摩擦力Ffm=6.0N,绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m=1.0kg的小球,当转台以ω=5.0rad/s的角速度转动时,欲使木块相对转台静止,则它到O孔的距离不可能是( )
如图所示,在水平转台上放一个质量M=2.0kg的木块,它与台面间的最大静摩擦力Ffm=6.0N,绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m=1.0kg的小球,当转台以ω=5.0rad/s的角速度转动时,欲使木块相对转台静止,则它到O孔的距离不可能是( )
 如图所示,在水平转台上放一个质量M=2.0kg的木块,它与台面间的最大静摩擦力Ffm=6.0N,绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m=1.0kg的小球,当转台以ω=5.0rad/s的角速度转动时,欲使木块相对转台静止,则它到O孔的距离不可能是( )
如图所示,在水平转台上放一个质量M=2.0kg的木块,它与台面间的最大静摩擦力Ffm=6.0N,绳的一端系住木块,另一端穿过转台的中心孔O(为光滑的)悬吊一质量m=1.0kg的小球,当转台以ω=5.0rad/s的角速度转动时,欲使木块相对转台静止,则它到O孔的距离不可能是( )| A. | 6 cm | B. | 15 cm | C. | 30 cm | D. | 34 cm |
1.下列说法正确的有( )
| A. | 曲线运动也可能是匀变速运动 | |
| B. | 曲线运动的速度一定是要改变的 | |
| C. | 变速运动一定是曲线运动 | |
| D. | 速度大小不变的曲线运动是匀速运动,是没有加速度的 |
10.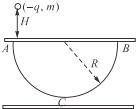 如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )
如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )
 如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )
如图所示,平行板电容器的两个极板水平,两板之间固定一个光滑绝缘的半圆形轨道ACB,A、B为半圆轨道的两个端点,且A、B紧靠电容器的上极板,在A端对应位置的极板处开有一个小孔,C是轨道的最低点,半圆轨道半径为R.现使电容器的两板分别带等量异种电荷,使两板之间存在竖直向下的匀强电场,将一个质量为m、电荷量为-q的带电小球,从A点正上方高为H处由静止释放,小球由小孔进入电容器内部并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,下列说法中正确的是( )| A. | 当匀强电场的电场强度大小E=$\frac{mg}{q}$时,带电小球在半圆形轨道内做匀速圆周运动 | |
| B. | 当匀强电场的电场强度大小E≤$\frac{mg(H+R)}{qR}$时,带电小球能沿轨道到达最低点 | |
| C. | 当匀强电场的电场强度大小E≤$\frac{mg(H+R)}{3qR}$时,带电小球能沿轨道到达最低点 | |
| D. | 将电容器的下极板向下移动一小段距离,则带电小球到达最低点C时的速率增大 |
14.用电器电阻值为R距交变电源L,输电线电流为I,电阻率为ρ,要求输电线上电压降不超过U.则输电线截面积最小值为( )
| A. | $\frac{ρL}{R}$ | B. | $\frac{2ρLI}{U}$ | C. | $\frac{U}{ρLI}$ | D. | $\frac{2UL}{ρI}$ |
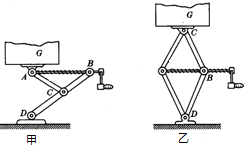 如图所示是汽年内常备的两种类型的“千斤顶”,是用于汽车换轮胎的顶升机,甲是“Y形”的,乙是“菱形”的,顺时钟摇动手柄,使螺旋杆转动,A,B间距离变小,重物G就被顶升起来,反之则可使G下降,若顶升的是汽车本身,便能进行换轮胎的操作了,若物重为G,AB与AC间的夹角为θ,此时螺杆AB的拉力为多少?
如图所示是汽年内常备的两种类型的“千斤顶”,是用于汽车换轮胎的顶升机,甲是“Y形”的,乙是“菱形”的,顺时钟摇动手柄,使螺旋杆转动,A,B间距离变小,重物G就被顶升起来,反之则可使G下降,若顶升的是汽车本身,便能进行换轮胎的操作了,若物重为G,AB与AC间的夹角为θ,此时螺杆AB的拉力为多少? 如图,已知电荷放q=3.0×10-10C的电荷,从A点移到B点,电场力做了6.0×10-8J的功.问:
如图,已知电荷放q=3.0×10-10C的电荷,从A点移到B点,电场力做了6.0×10-8J的功.问: