题目内容
19. 如图,水平桌面上固定有光滑金属导轨MN、PQ,它们的夹角为45°,导轨的右端点N、Q通过细导线与导体棒cd连接,在水平导轨MN、PQ上有一根质量M=0.8kg的足够长的金属棒ab垂直于导轨PQ,初始位置与两根导轨的交点为E、F,且E、F之间的距离为L1=4m,水平导轨之间存在竖直向上的匀强磁场,磁感应强度B1=0.5T,导体棒cd水平放置,处于匀强磁场B2中,匀强磁场B2水平且垂直导体棒cd向内,B2=0.3T,导体棒cd的质量m=0.1kg,长l0=0.5m,电阻R=1.5Ω,其他电阻均不计,不计细导线对c、d点的作用力,金属棒ab在外力的作用下从EF处以一定的初速度向右做直线运动,导体棒cd始终保持静止,取g=10m/s2,求:
如图,水平桌面上固定有光滑金属导轨MN、PQ,它们的夹角为45°,导轨的右端点N、Q通过细导线与导体棒cd连接,在水平导轨MN、PQ上有一根质量M=0.8kg的足够长的金属棒ab垂直于导轨PQ,初始位置与两根导轨的交点为E、F,且E、F之间的距离为L1=4m,水平导轨之间存在竖直向上的匀强磁场,磁感应强度B1=0.5T,导体棒cd水平放置,处于匀强磁场B2中,匀强磁场B2水平且垂直导体棒cd向内,B2=0.3T,导体棒cd的质量m=0.1kg,长l0=0.5m,电阻R=1.5Ω,其他电阻均不计,不计细导线对c、d点的作用力,金属棒ab在外力的作用下从EF处以一定的初速度向右做直线运动,导体棒cd始终保持静止,取g=10m/s2,求:(1)金属棒ab在EF处的速度v1;
(2)金属棒ab从EF处向右运动距离d=2m的过程中通过ab的电荷量q和需要的时间t;
(3)金属棒ab从EF处向右运动距离d=2m外力做的功W.
分析 (1)导体棒cd处于平衡状态,根据共点力的平衡条件结合闭合电路的欧姆定律、法拉第电磁感应定律求解;
(2)根据法拉第电磁感应定律和闭合电路欧姆定律求解通过ab的电荷量q和需要的时间t;
(3)根据焦耳定律计算该过程中导体棒cd中产生的焦耳热,根据功能关系可得外力做的功W.
解答 解:(1)金属棒ab切割磁感应线产生的感应电动势为:
E=B1L1v1,
导体棒cd的电流为:I=$\frac{E}{R}$,
导体棒cd处于平衡状态,有:
B2Il0=mg,
联立并代入数据解得:v1=5m/s;
(2)由于导体棒cd始终静止,所以金属棒ab运动的过程中,感应电流不变,感应电动势不变,根据法拉第电磁感应定律可得:
E=$\frac{△Φ}{t}$=$\frac{{B}_{1}△S}{t}$,
通过ab的电荷量为:q=It=$\frac{E}{R}t$=$\frac{△Φ}{R}=\frac{{B}_{1}△S}{R}$,
向右运动距离d=2m时切割磁感应线的有效长度为:
L2=$\frac{1}{2}{L}_{1}=2m$,
△S=$\frac{1}{2}({L}_{1}+{L}_{2})d=6{m}^{2}$,
解得:q=2C,t=0.3s;
(3)该过程中导体棒cd中产生的焦耳热为:Q=I2Rt=$\frac{{E}^{2}}{R}t$,
代入数据解得:Q=20J;
金属棒从EF处向左运动距离d=20m时,有:E=B1L2v2,
可得此时的速度为:v2=10m/s,
该过程中根据功能关系可得:W=Q+$\frac{1}{2}M{v}_{2}^{2}-\frac{1}{2}M{v}_{1}^{2}$,
解得:W=50J.
答:(1)金属棒ab在EF处的速度为5m/s;
(2)金属棒ab从EF处向右运动距离d=2m的过程中通过ab的电荷量q为2C,需要的时间t为0.3s;
(3)金属棒ab从EF处向右运动距离d=2m外力做的功为50J.
点评 对于电磁感应问题研究思路常常有两条:一条从力的角度,重点是分析安培力作用下物体的平衡问题;另一条是能量,分析电磁感应现象中的能量如何转化是关键.

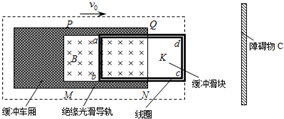 如图所示,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块K和质量为m的缓冲车厢.在缓冲车厢的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN,缓冲车厢的底部安装电磁铁(未画出),能产生垂直于导轨平面向下的匀强磁场,磁场的磁感应强度大小为B.导轨内的缓冲滑块K由高强度绝缘材料制成,滑块K上绕有闭合矩形线圈abcd,线圈的总电阻为R、匝数为n,ab边长为L.假设缓冲车厢以速度v0与障碍物C碰撞后,滑块K立即停下,而缓冲车厢继续向前移动距离L后速度为零.已知缓冲车厢与障碍物、缓冲车厢与线圈的ab边均没有接触,不计一切摩擦阻力.在这个缓冲过程中,下列说法正确的是( )
如图所示,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块K和质量为m的缓冲车厢.在缓冲车厢的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN,缓冲车厢的底部安装电磁铁(未画出),能产生垂直于导轨平面向下的匀强磁场,磁场的磁感应强度大小为B.导轨内的缓冲滑块K由高强度绝缘材料制成,滑块K上绕有闭合矩形线圈abcd,线圈的总电阻为R、匝数为n,ab边长为L.假设缓冲车厢以速度v0与障碍物C碰撞后,滑块K立即停下,而缓冲车厢继续向前移动距离L后速度为零.已知缓冲车厢与障碍物、缓冲车厢与线圈的ab边均没有接触,不计一切摩擦阻力.在这个缓冲过程中,下列说法正确的是( )| A. | 线圈中的感应电流沿逆时针方向(俯视),且最大感应电流为$\frac{nBL{v}_{0}}{R}$ | |
| B. | 轨道受到的磁场作用力使缓冲车厢减速运动,从而实现缓冲 | |
| C. | 此过程中,通过线圈abcd的电荷量为$\frac{nB{L}^{2}}{R}$ | |
| D. | 此过程中,线圈abcd产生的焦耳热为$\frac{1}{2}$mv02 |
| A. | 飞向茫茫宇宙 | B. | 成为地球的同步“苹果卫星” | ||
| C. | 成为地球的“苹果月亮” | D. | 落向地面 |
 根据玻尔原子结构理论,氦离子(He+)的能级图如图所示.当某个He+处在n=4的激发态时,由于跃迁所释放的光子不可能有( )
根据玻尔原子结构理论,氦离子(He+)的能级图如图所示.当某个He+处在n=4的激发态时,由于跃迁所释放的光子不可能有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 6个 |
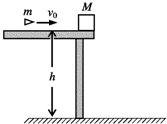 如图所示,一质量M=1.2kg的物块静止在桌面边缘.桌面离地面的高度h=1.8m,一质量m=20g的子弹以水平速度v0=200m/s射人物块,并在很短的时间内水平穿出,已知物块落地点离桌面边缘的水平距离x=1.2m,g取10m/s2.求:
如图所示,一质量M=1.2kg的物块静止在桌面边缘.桌面离地面的高度h=1.8m,一质量m=20g的子弹以水平速度v0=200m/s射人物块,并在很短的时间内水平穿出,已知物块落地点离桌面边缘的水平距离x=1.2m,g取10m/s2.求: (1)在用单摆测定重力加速度的实验中,下列措施中必要的或做法正确的是BCD.
(1)在用单摆测定重力加速度的实验中,下列措施中必要的或做法正确的是BCD.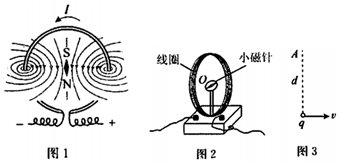

 如图所示,间距为L平行且足够长的光滑导轨由两部分组成:倾斜部分与水平部分平滑相连,倾角为θ,在倾斜导轨顶端连接一阻值为r的定值电阻.质量为m、电阻也为r的金属杆MN垂直导轨跨放在导轨上,在倾斜导轨区域加以垂直导轨平面向下、磁感应强度为B的匀强磁场;在水平导轨区域加另一垂直轨道平面向下、磁感应强度也为B的匀强磁场.闭合开关S,让金属杆MN从图示位置由静止释放,已知金属杆运动到水平轨道前,已达到最大速度,不计导轨电阻且金属杆始终与导轨接触良好,重力加速度为g.求:
如图所示,间距为L平行且足够长的光滑导轨由两部分组成:倾斜部分与水平部分平滑相连,倾角为θ,在倾斜导轨顶端连接一阻值为r的定值电阻.质量为m、电阻也为r的金属杆MN垂直导轨跨放在导轨上,在倾斜导轨区域加以垂直导轨平面向下、磁感应强度为B的匀强磁场;在水平导轨区域加另一垂直轨道平面向下、磁感应强度也为B的匀强磁场.闭合开关S,让金属杆MN从图示位置由静止释放,已知金属杆运动到水平轨道前,已达到最大速度,不计导轨电阻且金属杆始终与导轨接触良好,重力加速度为g.求: