题目内容
9.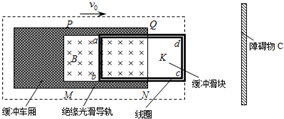 如图所示,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块K和质量为m的缓冲车厢.在缓冲车厢的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN,缓冲车厢的底部安装电磁铁(未画出),能产生垂直于导轨平面向下的匀强磁场,磁场的磁感应强度大小为B.导轨内的缓冲滑块K由高强度绝缘材料制成,滑块K上绕有闭合矩形线圈abcd,线圈的总电阻为R、匝数为n,ab边长为L.假设缓冲车厢以速度v0与障碍物C碰撞后,滑块K立即停下,而缓冲车厢继续向前移动距离L后速度为零.已知缓冲车厢与障碍物、缓冲车厢与线圈的ab边均没有接触,不计一切摩擦阻力.在这个缓冲过程中,下列说法正确的是( )
如图所示,虚线框内为某种电磁缓冲车的结构示意图,其主要部件为缓冲滑块K和质量为m的缓冲车厢.在缓冲车厢的底板上,沿车的轴线固定着两个光滑水平绝缘导轨PQ、MN,缓冲车厢的底部安装电磁铁(未画出),能产生垂直于导轨平面向下的匀强磁场,磁场的磁感应强度大小为B.导轨内的缓冲滑块K由高强度绝缘材料制成,滑块K上绕有闭合矩形线圈abcd,线圈的总电阻为R、匝数为n,ab边长为L.假设缓冲车厢以速度v0与障碍物C碰撞后,滑块K立即停下,而缓冲车厢继续向前移动距离L后速度为零.已知缓冲车厢与障碍物、缓冲车厢与线圈的ab边均没有接触,不计一切摩擦阻力.在这个缓冲过程中,下列说法正确的是( )| A. | 线圈中的感应电流沿逆时针方向(俯视),且最大感应电流为$\frac{nBL{v}_{0}}{R}$ | |
| B. | 轨道受到的磁场作用力使缓冲车厢减速运动,从而实现缓冲 | |
| C. | 此过程中,通过线圈abcd的电荷量为$\frac{nB{L}^{2}}{R}$ | |
| D. | 此过程中,线圈abcd产生的焦耳热为$\frac{1}{2}$mv02 |
分析 根据楞次定律判断感应电流的方向,由法拉第定律和欧姆定律结合求解最大感应电流.由q=n $\frac{△Φ}{R}$求解通过线圈abcd的电荷量.根据能量守恒求解线圈abcd产生的焦耳热.
解答 解:A、缓冲车以速度v0与障碍物C碰撞后,滑块K立即停下,穿过线圈abcd的磁通量增大,由楞次定律知线圈中的感应电流沿逆时针方向.滑块相对磁场的最大速度大小为v0,线圈中产生的感应电动势最大值为 Em=nBLv0.感应电流最大为 Im=$\frac{nBL{v}_{0}^{\;}}{R}$,故A正确.
B、根据左手定则可知,磁场对线圈abcd有向右的安培力作用,则线圈abcd对磁场,即对缓冲车厢向左安培力,使缓冲车厢减速运动,从而实现缓冲.故B正确.
C、此过程线圈abcd中通过的电量:q=n $\frac{△Φ}{R}$=n $\frac{B{L}_{\;}^{2}}{R}$,故C正确.
D、由功能关系得线圈产生的焦耳热为:Q=$\frac{1}{2}$mv02.故D正确.
故选:ABCD
点评 本题考查学生分析和理解科技成果的能力,运用电磁感应、电路及力学的基本规律进行分析和解答.注意线圈的匝数不能遗漏.对于感应电荷量经验公式q=n $\frac{△Φ}{R}$,要在理解的基础上记牢经常用到.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
19.密利根说:“科学靠两条腿走路,一是理论,二是实验.有时一条腿走在前面,有时另一条腿走在后面,但只有使用两条腿,才能前进”.下列说法中不正确的是( )
| A. | 康普顿效应和电子的衍射现象说明粒子的波动性 | |
| B. | 法拉第首先提出了“场”的概念,发现了电磁感应现象 | |
| C. | β衰变的实质是核内的中子转化成了一个质子和一个电子,而且其半衰期与原子所受的化学状态和外部条件无关 | |
| D. | 根据玻尔的氢原子模型可知,一群氢原子处在n=4的能级,当它跃迁到较低能级时,最多可发出6种频率的光子 |
20.下列说法中正确的是( )
| A. | 物体的温度升高时,其内部分子的平均动能一定变大 | |
| B. | 气体的压强越大,其分子运动得一定越剧烈 | |
| C. | 气体的压强越大,其分子之间的斥力一定越大 | |
| D. | 分子间距离减小,分子间的势能也一定减小 |
17.下列说法中正确的是( )
| A. | 无论入射光的频率如何,只要该入射光照射金属的时间足够长,就一定能产生光电效应 | |
| B. | 氢原子的核外电子,由离核较远的轨道自发跃迁到离核较近的轨道的过程中,放出光子,电子动能减小,原子的电势能减小 | |
| C. | 天然放射现象的发现揭示了原子核有复杂的结构 | |
| D. | 核力存在于原子核内的所有核子之间 |
14. 如图所示一质量为M的斜面体静止在水平地面上,物体B在沿斜面向上的力F作用下沿斜面匀速上滑,A、B之同的动摩擦因数为μ,μ<tanθ,且质量均为m,则( )
如图所示一质量为M的斜面体静止在水平地面上,物体B在沿斜面向上的力F作用下沿斜面匀速上滑,A、B之同的动摩擦因数为μ,μ<tanθ,且质量均为m,则( )
 如图所示一质量为M的斜面体静止在水平地面上,物体B在沿斜面向上的力F作用下沿斜面匀速上滑,A、B之同的动摩擦因数为μ,μ<tanθ,且质量均为m,则( )
如图所示一质量为M的斜面体静止在水平地面上,物体B在沿斜面向上的力F作用下沿斜面匀速上滑,A、B之同的动摩擦因数为μ,μ<tanθ,且质量均为m,则( )| A. | A、B保持相对静止 | |
| B. | 地面对斜面体的摩擦力等于Fcosθ | |
| C. | 地面受到的压力小于(M+2m)g | |
| D. | B与斜面间的动摩擦因数为$\frac{F-mgsinθ-μmgcosθ}{2mgcosθ}$ |
1. 如图所示,倾角为30°、高为L的固定斜面底端与水平光滑相连,质量分别为3m、m的两个小球A、B(可视为质点)用长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞时间极短并无机械能损失.且碰后只能沿斜面下滑,两球最终均滑到水平面上并发生碰撞粘在一起继续运动,不计一切摩擦,则( )
如图所示,倾角为30°、高为L的固定斜面底端与水平光滑相连,质量分别为3m、m的两个小球A、B(可视为质点)用长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞时间极短并无机械能损失.且碰后只能沿斜面下滑,两球最终均滑到水平面上并发生碰撞粘在一起继续运动,不计一切摩擦,则( )
 如图所示,倾角为30°、高为L的固定斜面底端与水平光滑相连,质量分别为3m、m的两个小球A、B(可视为质点)用长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞时间极短并无机械能损失.且碰后只能沿斜面下滑,两球最终均滑到水平面上并发生碰撞粘在一起继续运动,不计一切摩擦,则( )
如图所示,倾角为30°、高为L的固定斜面底端与水平光滑相连,质量分别为3m、m的两个小球A、B(可视为质点)用长为L的轻绳连接,A球置于斜面顶端.现由静止释放A、B两球,B球与弧形挡板碰撞时间极短并无机械能损失.且碰后只能沿斜面下滑,两球最终均滑到水平面上并发生碰撞粘在一起继续运动,不计一切摩擦,则( )| A. | A球到达斜面底端的速率为$\frac{\sqrt{5gL}}{2}$ | |
| B. | B球到达斜面底端的速率为$\frac{\sqrt{6gL}}{2}$ | |
| C. | A球沿斜面下滑的过程中,轻绳一直对B球做正功 | |
| D. | 两球粘在一起运动后的速率为$\frac{3(\sqrt{5}+1)}{8}$$\sqrt{gL}$ |
18. 如图所示,质量均为m,长度均为L的完全相同的甲、乙两木板静止在足够长的光滑水平面上,可视为质点的质量M=2m的小铁块以速度v0从左端冲上甲木板,当甲、乙两木板分离时,甲木板的速度为$\frac{1}{3}$v0,最终小铁块未从乙木板上滑下.已知小铁块与木板间的动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )
如图所示,质量均为m,长度均为L的完全相同的甲、乙两木板静止在足够长的光滑水平面上,可视为质点的质量M=2m的小铁块以速度v0从左端冲上甲木板,当甲、乙两木板分离时,甲木板的速度为$\frac{1}{3}$v0,最终小铁块未从乙木板上滑下.已知小铁块与木板间的动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )
 如图所示,质量均为m,长度均为L的完全相同的甲、乙两木板静止在足够长的光滑水平面上,可视为质点的质量M=2m的小铁块以速度v0从左端冲上甲木板,当甲、乙两木板分离时,甲木板的速度为$\frac{1}{3}$v0,最终小铁块未从乙木板上滑下.已知小铁块与木板间的动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )
如图所示,质量均为m,长度均为L的完全相同的甲、乙两木板静止在足够长的光滑水平面上,可视为质点的质量M=2m的小铁块以速度v0从左端冲上甲木板,当甲、乙两木板分离时,甲木板的速度为$\frac{1}{3}$v0,最终小铁块未从乙木板上滑下.已知小铁块与木板间的动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )| A. | 小铁块最终与乙木板共速,两者的速度为$\frac{1}{9}$v0 | |
| B. | 从小铁块滑上乙木板到两者刚好相对静止,共用时为$\frac{{v}_{0}}{9μg}$ | |
| C. | 当小铁块与乙木板刚好共速时,两木板间的距离为$\frac{4{v}_{0}}{81μg}$ | |
| D. | 小铁块最终停在距乙木板左端$\frac{L}{12}$处 |
 如图所示,足够长且电阻不计的光滑导轨PQ、MN相距d=1m,其与水平面夹角为α,整个导轨所在区域有匀强磁场,磁场方向垂直于导轨平面斜向上;长为1m的金属棒ab垂直于导轨放置,且接触良好,金属棒质量为0.1kg且电阻r=1Ω;导轨右侧电路中灯泡的电阻RL=3Ω、定值电阻R1=7Ω;现调节电阻箱使R2=6Ω,在t=0时刻由静止释放ab,t=0.25s时刻闭合开关S,此时金属棒的速度v1=1.5m/s,此后ab棒做变加速运动且最终以v2=6m/s做匀速直线运动,重力加速度大小g=10m/s2.
如图所示,足够长且电阻不计的光滑导轨PQ、MN相距d=1m,其与水平面夹角为α,整个导轨所在区域有匀强磁场,磁场方向垂直于导轨平面斜向上;长为1m的金属棒ab垂直于导轨放置,且接触良好,金属棒质量为0.1kg且电阻r=1Ω;导轨右侧电路中灯泡的电阻RL=3Ω、定值电阻R1=7Ω;现调节电阻箱使R2=6Ω,在t=0时刻由静止释放ab,t=0.25s时刻闭合开关S,此时金属棒的速度v1=1.5m/s,此后ab棒做变加速运动且最终以v2=6m/s做匀速直线运动,重力加速度大小g=10m/s2. 如图,水平桌面上固定有光滑金属导轨MN、PQ,它们的夹角为45°,导轨的右端点N、Q通过细导线与导体棒cd连接,在水平导轨MN、PQ上有一根质量M=0.8kg的足够长的金属棒ab垂直于导轨PQ,初始位置与两根导轨的交点为E、F,且E、F之间的距离为L1=4m,水平导轨之间存在竖直向上的匀强磁场,磁感应强度B1=0.5T,导体棒cd水平放置,处于匀强磁场B2中,匀强磁场B2水平且垂直导体棒cd向内,B2=0.3T,导体棒cd的质量m=0.1kg,长l0=0.5m,电阻R=1.5Ω,其他电阻均不计,不计细导线对c、d点的作用力,金属棒ab在外力的作用下从EF处以一定的初速度向右做直线运动,导体棒cd始终保持静止,取g=10m/s2,求:
如图,水平桌面上固定有光滑金属导轨MN、PQ,它们的夹角为45°,导轨的右端点N、Q通过细导线与导体棒cd连接,在水平导轨MN、PQ上有一根质量M=0.8kg的足够长的金属棒ab垂直于导轨PQ,初始位置与两根导轨的交点为E、F,且E、F之间的距离为L1=4m,水平导轨之间存在竖直向上的匀强磁场,磁感应强度B1=0.5T,导体棒cd水平放置,处于匀强磁场B2中,匀强磁场B2水平且垂直导体棒cd向内,B2=0.3T,导体棒cd的质量m=0.1kg,长l0=0.5m,电阻R=1.5Ω,其他电阻均不计,不计细导线对c、d点的作用力,金属棒ab在外力的作用下从EF处以一定的初速度向右做直线运动,导体棒cd始终保持静止,取g=10m/s2,求: