��Ŀ����
20�� ��ͼ��ʾ�������㹻���Ĺ⻬ƽ�н�������MN��PQ�����ΪL������費�ƣ������켰�乹�ɵ�ƽ����ˮƽ��ɦȽǣ�������ϸ�����ӵĽ�����ab��cd�ֱ�ֱ������ã�ƽ��б�����ϵ�����F�����ڸ�ab�ϣ�ʹ���˾�ֹ����֪��������ab��cd�������ֱ�Ϊm��2m���������˵��ܵ���ΪR�����Һ͵���ʼ�ձ������ýӴ�������װ�ô��ڴ�ֱ�ڵ���ƽ�����ϵ���ǿ�ų��У��Ÿ�Ӧǿ��ΪB��ijʱ�̽�ϸ���նϣ�����F��������
��ͼ��ʾ�������㹻���Ĺ⻬ƽ�н�������MN��PQ�����ΪL������費�ƣ������켰�乹�ɵ�ƽ����ˮƽ��ɦȽǣ�������ϸ�����ӵĽ�����ab��cd�ֱ�ֱ������ã�ƽ��б�����ϵ�����F�����ڸ�ab�ϣ�ʹ���˾�ֹ����֪��������ab��cd�������ֱ�Ϊm��2m���������˵��ܵ���ΪR�����Һ͵���ʼ�ձ������ýӴ�������װ�ô��ڴ�ֱ�ڵ���ƽ�����ϵ���ǿ�ų��У��Ÿ�Ӧǿ��ΪB��ijʱ�̽�ϸ���նϣ�����F����������1�������ٶ�δ�����ǰ��ab��cd���˵ļ��ٶȵĴ�С֮�ȣ�
��2�������ٶ����ʱ����·�еĵ繦�ʣ�
���� ��1�����������������ն�ϸ��ǰ�������Ĵ�С���ն�ϸ�ߺ�ͨ�������ĵ�����С��ȣ���������С��ȣ�����ţ�ٵڶ�����������ٶ�֮�ȣ�
��2����ab����cd�����ٶ�Ϊ��ʱ���ٶȾ������������ƽ�⣬��ϱպϵ�·ŷķ���ɼ����ʱ���ʽ����
��� �⣺��1�����˾�ֹʱ��m+2m��gsin��=F
�ն�ϸ�ߺ�ab��cd�˵��ٶȴ��·ֱ�Ϊv1��v2�����ٶȴ�С�ֱ�Ϊa1��a2
E=BL��v1+v2��
I=$\frac{E}{R}$
��֪ab��cd���ܵ��İ�������С��ȣ�
F-mgsin��-F��=ma1
2mgsin��-F��=2ma2
�������$\frac{{a}_{1}}{{a}_{2}}=\frac{2}{1}$
��2���������˵İ�������С��ȣ������ٶ�Ϊ��ʱ�ٶȵ������
����cd
2mgsin��-BImL=0
$P{=I}_{m}^{2}R$
�������$P=\frac{4{m}^{2}{g}^{2}Rsi{n}^{2}��}{{B}^{2}{L}^{2}}$
�𣺣�1�������ٶ�δ�����ǰ��ab��cd���˵ļ��ٶȵĴ�С֮��Ϊ2��1��
��2�������ٶ����ʱ����·�еĵ繦��$\frac{4{m}^{2}{g}^{2}Rsi{n}^{2}��}{{B}^{2}{L}^{2}}$
���� �����ۺϿ�����ţ�ٵڶ����ɡ��պϵ�·ŷķ���ɡ��ۺ���ǿ��������ѵ���˫��ģ�ͣ������и������Ӧ�綯��

 ��ͼ��ʾΪ���м�г�Შ��ͬһ���ϴ�����t=0ʱ�̵IJ���ͼ����֪�ײ����Ҵ����Ҳ���������˵����ȷ���ǣ�������
��ͼ��ʾΪ���м�г�Შ��ͬһ���ϴ�����t=0ʱ�̵IJ���ͼ����֪�ײ����Ҵ����Ҳ���������˵����ȷ���ǣ�������| A�� | �ײ���Ƶ�ʱ��Ҳ���Ƶ�ʴ� | |
| B�� | ���в�ͬʱ��������ԭ�� | |
| C�� | ��������������ȣ������в�����ʱ���ᷢ���������� | |
| D�� | x=0.5cm�����ʵ㿪ʼ��ʱ�ķ�����+y���� | |
| E�� | ���в�����ʱx=0��Ϊ������ |
 ijͬѧ����̽�������͵����쳤�Ĺ�ϵ��ʵ��ʱ���������ͼ����ʾ��ʵ��װ�ã����õĹ������������30g�����Ȳ�����ҹ���ʱ���ɵij��ȣ��ٽ�5������������ڵ��ɵ��¶ˣ�ÿ�ζ������Ӧ�ĵ����ܳ��ȣ�����������������ı��У�������ʼ��δ���������ȣ�ȡg=10m/s2��
ijͬѧ����̽�������͵����쳤�Ĺ�ϵ��ʵ��ʱ���������ͼ����ʾ��ʵ��װ�ã����õĹ������������30g�����Ȳ�����ҹ���ʱ���ɵij��ȣ��ٽ�5������������ڵ��ɵ��¶ˣ�ÿ�ζ������Ӧ�ĵ����ܳ��ȣ�����������������ı��У�������ʼ��δ���������ȣ�ȡg=10m/s2��| ��������M��g�� | 0 | 30 | 60 | 90 | 120 | 150 |
| ���ɵ���L��cm�� | 6.00 | 7.15 | 8.34 | 9.48 | 10.46 | 11.79 |
��2������һ������ͼ�߿ɵý��ۣ����ɵĵ�����С�͵����쳤����С������
��3���õ��ɾ���ϵ��k=25N/m�����������λ��Ч���֣���
 ��ѧ�����ϼ������з������γ���30����ǰ�Ļ�����ʯ�������з����˹�ȥ���������������˻�����ʯ����쳣�����1�£��й�����������2011��7����Ħ��������ʯ��֤ʵ���Ի��ǣ�ijͬѧ�ƻ�����ƽʱ�ռ��Ļ������ϣ���ͼ��ʾ����������ǵ��ܶȣ����������ʯ���ܶȽ��бȽ���֤�����м�������ܶȵĹ�ʽ��ȷ���ǣ�GΪ�����������������Ի�����ת��Ӱ�죬��������Ϊ���壩��������
��ѧ�����ϼ������з������γ���30����ǰ�Ļ�����ʯ�������з����˹�ȥ���������������˻�����ʯ����쳣�����1�£��й�����������2011��7����Ħ��������ʯ��֤ʵ���Ի��ǣ�ijͬѧ�ƻ�����ƽʱ�ռ��Ļ������ϣ���ͼ��ʾ����������ǵ��ܶȣ����������ʯ���ܶȽ��бȽ���֤�����м�������ܶȵĹ�ʽ��ȷ���ǣ�GΪ�����������������Ի�����ת��Ӱ�죬��������Ϊ���壩��������| A�� | ��=$\frac{3{g}_{0}}{��Gd}$ | B�� | ��=$\frac{{g}_{0}{T}^{2}}{3��d}$ | C�� | ��=$\frac{3��}{G{T}^{2}}$ | D�� | ��=$\frac{6M}{��{d}^{3}}$ |
 ��ͼ����ij��ɫ��������ܵ�����K���ᷢ�����ЧӦ��������A������K֮����Ϸ����ѹ��ͨ�����ڻ����������Ļ�Ƭ��������ڹ����ϵĵ�ѹ��ֱ���������е���ǡΪ�㣬��ʱ��ѹ���ĵ�ѹֵU��Ϊ�����ֹ��ѹ���ֱַ���Ƶ��Ϊv1��v2�ĵ�ɫ��������������÷����ֹ��ѹ�ֱ�ΪU1��U2������ӵ�����Ϊm�������Ϊe�������й�ϵʽ��ȷ���ǣ�������
��ͼ����ij��ɫ��������ܵ�����K���ᷢ�����ЧӦ��������A������K֮����Ϸ����ѹ��ͨ�����ڻ����������Ļ�Ƭ��������ڹ����ϵĵ�ѹ��ֱ���������е���ǡΪ�㣬��ʱ��ѹ���ĵ�ѹֵU��Ϊ�����ֹ��ѹ���ֱַ���Ƶ��Ϊv1��v2�ĵ�ɫ��������������÷����ֹ��ѹ�ֱ�ΪU1��U2������ӵ�����Ϊm�������Ϊe�������й�ϵʽ��ȷ���ǣ�������| A�� | Ƶ��Ϊv1�Ĺ�����ʱ������ӵ������ٶ�Ϊ$\sqrt{\frac{2e{U}_{1}}{m}}$ | |
| B�� | ����K�������ݳ���Ϊhv1 | |
| C�� | ����K�����ļ���Ƶ����$\frac{{U}_{2}{v}_{1}-{U}_{1}{v}_{2}}{{U}_{1}-{U}_{2}}$ | |
| D�� | ���ʿ˳���h=$\frac{e��{U}_{1}-{U}_{2}��}{{v}_{1}-{v}_{2}}$ |
 ��ͼ��ʾ��ˮƽ���ϵ�С�������˶���ϵ�ڳ���Ե�������ƹ������֣���������Ϊm��������������С����v1���ٶ�����ֱ���˶��������������ˮƽ����ļн�Ϊ��ʱ��������ٶ�Ϊv2�������й�ϵʽ��ȷ���ǣ�������
��ͼ��ʾ��ˮƽ���ϵ�С�������˶���ϵ�ڳ���Ե�������ƹ������֣���������Ϊm��������������С����v1���ٶ�����ֱ���˶��������������ˮƽ����ļн�Ϊ��ʱ��������ٶ�Ϊv2�������й�ϵʽ��ȷ���ǣ�������| A�� | v2=v1 | B�� | v2=v1��cos�� | C�� | v2=0 | D�� | v2=$\frac{{v}_{1}}{cos��}$ |
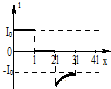
 ��ͼ1��n��Բ���߿�̶�����ǿ�ų��У��Ÿ��ߵķ����뵼�߿�����ƽ�洹ֱ���涨�ų���������ֱֽ������Ÿ�Ӧǿ��B��ʱ��仯�Ĺ�����ͼ2��ʾ�����涨˳ʱ�뷽��Ϊ��Ӧ����i�����������и�ͼ����ȷ���ǣ�������
��ͼ1��n��Բ���߿�̶�����ǿ�ų��У��Ÿ��ߵķ����뵼�߿�����ƽ�洹ֱ���涨�ų���������ֱֽ������Ÿ�Ӧǿ��B��ʱ��仯�Ĺ�����ͼ2��ʾ�����涨˳ʱ�뷽��Ϊ��Ӧ����i�����������и�ͼ����ȷ���ǣ�������



 ��ͼabcdΪһ�߳�ΪL�����������ĸ��Ե��߿�bc�ߴ��ӵ���R�����ߵ��費�ƣ�����Ϊ��ǿ�ų��ı߽磬����Ϊ2L���Ÿ�Ӧǿ��ΪB��������ֱ
��ͼabcdΪһ�߳�ΪL�����������ĸ��Ե��߿�bc�ߴ��ӵ���R�����ߵ��費�ƣ�����Ϊ��ǿ�ų��ı߽磬����Ϊ2L���Ÿ�Ӧǿ��ΪB��������ֱ


 ��ͼ��ʾ���⻬ˮƽ����������Сľ��A��B��C�����ǵ������ֱ���mA=2kg��mB=2kg��mC=3kg��BC�м���һ�����ʵ�����������v0=14m/s���ٶ��ڼ���ʱ����B��������ϳ�һ���壮��ϵͳ�˶�������Сľ��A����С���ܣ�
��ͼ��ʾ���⻬ˮƽ����������Сľ��A��B��C�����ǵ������ֱ���mA=2kg��mB=2kg��mC=3kg��BC�м���һ�����ʵ�����������v0=14m/s���ٶ��ڼ���ʱ����B��������ϳ�һ���壮��ϵͳ�˶�������Сľ��A����С���ܣ�