��Ŀ����
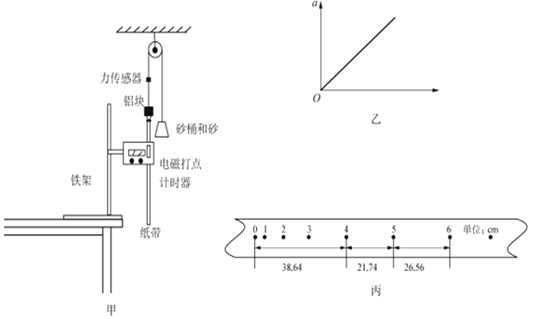
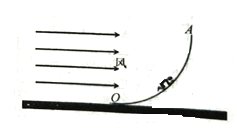
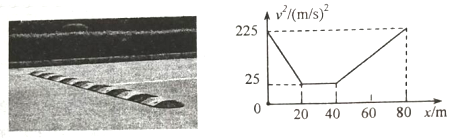
����Ŀ������ֱƽ���ڣ����⻬������OP�����ͼ��ʾ��״��PQΪһ����ˮƽ����н�Ϊ37���Ĵֲ�ֱ�ˣ�������ƽ�����ӡ�С�����ڽ������ϣ�����x��0����v0��5m/s�ij��ٶ��ظ��˶�����ֱ֪���㹻����С����ֱ�˼�Ķ�Ħ������Ϊ�̣�0.5��gȡ10m/s2��sin37�㣽0.6��cos37�㣽0.8����
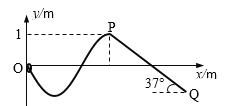
��1��С���˶���P��ʱ���ٶȴ�Сv��
��2��С����ֱ�����˶�ʱ�ļ��ٶȴ�Сa��
��3����y��0��Ϊ�������棬��С����ֱ�����˶�ʱ�����ܺ�����������ȵ�λ�ã�ֻ�����y�����꣩��
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
�����������������С����OP�����˶�ʱ���������͵������ã���ֻ����������������С����е���غ㼴������ٶȣ���С����ֱ���ϵ������������ţ�ٵڶ����ɼ���������ٶȣ�Ӧ���˶�ѧ��ʽ�Ͷ��ܶ�������������ܺ�����������ȵ�λ����
��1��С����OP�����˶�ʱ���������͵������ã���ֻ������������
С����е���غ㣬��y��0��Ϊ�������棬��![]()
�������ݣ���v��![]() m/s
m/s
��2��С����ֱ���ϵ�������ͼ��ʾ��
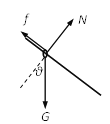
��ţ�ٶ��ɣ�mgsin37�㣭f ��ma
N��mgcos37�� �� f ����N
�������ݿɵã�a��2m/s2
��3��������y����Ek��Ep ����![]()
���ȼ����˶���ʽ��v2��v2��2aS
����![]()
�������ݣ��ɵ�![]()

 ����������������ϵ�д�
����������������ϵ�д�