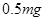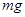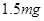题目内容
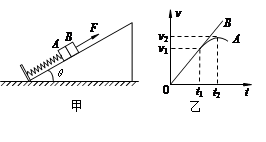
物体以v0的初速度从倾角为30°的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时，其动能减少了ΔEk=12J，机械能减少了ΔE=2J，不计空气阻力，重力加速度g=10m/s2，则物体沿斜坡向下运动时加速度大小为
| A．2m/s2 | B．3m/s2 | C．4m/s2 | D．6m/s2 |
C
解析试题分析：假设上述过程在斜面上滑行的位移是x，摩擦阻力大小是f，由功能关系可知：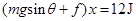
①
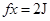②
联立①、②两式可得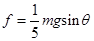
当物体下滑时，根据牛顿第二定律可得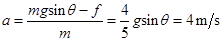
考点：牛顿定律的应用、功能关系、动能定理
练习册系列答案
相关题目
如图所示，三角体由两种材料拼接而成，BC界面平行底面DE，且B点为AD的中点，两侧面与水平面夹角分别为37
。和53。已知一物块从A静止下滑，加速至B减速至D，且到D点时恰好静止。若该物块从A点静止释放沿另一侧面下滑，则有 （ ）
| A．通过C点的速率大于通过B点的速率 |
| B．AC段加速，CE段减速 |
| C．到达E点时速度大于零 |
| D．一直加速运动到E，但AC段的加速度比CE段小 |
如图所示，小车上固定一水平横杆，横杆左端的固定斜杆与竖直方向成α角，斜杆下端连接一质量为m的小球；横杆右端用一根细线悬挂相同的小球。当小车沿水平面做直线运动时，细线与竖直方向间的夹角β(β≠α)保持不变。设斜杆、细线对小球的作用力分别为F1、F2，下列说法正确的是( )
| A．F1、F2大小相等 | B．F1、F2方向相同 |
| C．小车加速度大小为gtanα | D．小车加速度大小为gtanβ |
如图所示，在倾角为α的固定光滑斜面上，有一用绳子拴着的长木板，木板上站着一只猫．已知木板的质量是猫的质量的2倍．当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变．则此时木板沿斜面下滑的加速度为 ( )
A．sin | B． | C．gsin | D．2gsin |
如图所示，平直木板AB倾斜放置，板上的P点距A端较近，小物体与木板之间的动摩擦因数由A到B逐渐减小。先让物体从A端由静止开始滑到B端，然后将A端着地，抬高B，使木板的倾角与前一过程相同，再让物体从B由静止开始下滑到A端。上述两过程相比较，下列说法中一定正确的是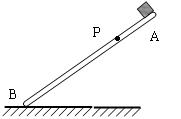
| A．物体经过P点的动能，前一过程较小 |
| B．物体从顶端滑到底端的时间，前一过程较长 |
| C．物体滑到底端时的速度，前一过程较大 |
| D．物体从顶端滑到P点的过程中因摩擦产生的热量，前一过程较少 |
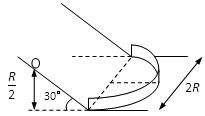
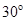的斜面连接水平面，在水平面上安装半径为
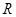的半圆竖直挡板，矢量
的小球从斜面上高为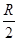
处静止释放到达水平面恰能贴着挡板内侧运动。不计小球体积，不计摩擦和机械能损失。则小球沿挡板运动时对挡板的力是（ ）
