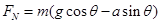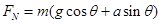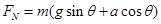题目内容
(12分)如图所示,宇航员从空间站C(绕地球运行)上释放了一颗质量m的探测卫星P 。该卫星通过一条柔软的细轻绳与空间站连接,稳定时卫星始终在空间站的正下方,到空间站的距离为l 。已知空间站的轨道为圆形,周期为T,地球半径为R,地球同步卫星到地面的高度为H0,地球自转周期为T0,万有引力常量为G,忽略卫星拉力对空间站轨道的影响,求:
(1)空间站离地面的高度H及卫星离地面的高度h;
(2)卫星所受轻绳拉力的大小。
(1)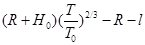 ;(2)
;(2)
解析试题分析:(1)设空间站离地面的高度为H, 因为同步卫星的周期和地球自转周期相同,根据开普勒第三定律以及题意有: ① ( 2分)
① ( 2分)
即: 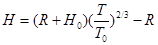 ② ( 2分)
② ( 2分)
卫星的高度: h =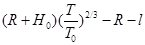 ③ ( 2分)
③ ( 2分)
(2)卫星在细绳的拉力 F 和地球引力作用下跟随空间站一起绕地球作周期为 T 的圆周运动,有: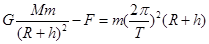 ④ ( 2分)
④ ( 2分)
式中 M为地球质量.空间站在地球引力作用下绕地球作周期为 T 的圆周运动
故有: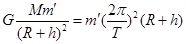 ⑤ ( 2分)
⑤ ( 2分)
式中m’为空间站的质量.由④、⑤两式得: ⑥ ( 2分)
⑥ ( 2分)
考点:万有引力定律及应用

 阅读快车系列答案
阅读快车系列答案如图所示,小车上有固定支架,支架上用细线拴一个小球,线长为l(小球可看作质点),小车与小球一起以速度v0沿水平方向向左匀速运动。当小车突然碰到矮墙后车立即停止运动,此后小球升高的最大高度可能是(线未被拉断)( )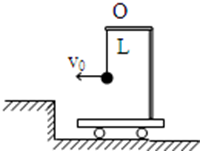
A.大于 | B.小于 |
C.等于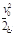 | D.等于2l |
物体以v0的初速度从倾角为30°的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时,其动能减少了ΔEk=12J,机械能减少了ΔE=2J,不计空气阻力,重力加速度g=10m/s2,则物体沿斜坡向下运动时加速度大小为
| A.2m/s2 | B.3m/s2 | C.4m/s2 | D.6m/s2 |
用力将重物竖直提起,先由静止开始匀加速上升,紧接着匀速上升。如果前后两过程的运动时间相同,不计空气阻力,则( )
| A.加速过程中拉力做的功比匀速过程中拉力做的功多 |
| B.匀速过程中拉力做的功比加速过程中拉力做的功多 |
| C.两过程中拉力做的功一样多 |
| D.上述三种情况都有可能 |
如图所示为阿特伍德设计的装置,不考虑绳与滑轮的质量,不计轴承摩擦、绳与滑轮间的摩擦。初始时两人均站在水平地面上;当位于左侧的甲用力向上攀爬时,位于右侧的乙始终用力抓住绳子,最终至少一人能到达滑轮。下列说法正确的是
| A.若甲的质量较大,则乙先到达滑轮 |
| B.若甲的质量较大,则甲、乙同时到达滑轮 |
| C.若甲、乙质量相同,则乙先到达滑轮 |
| D.若甲、乙质量相同,则甲先到达滑轮 |
如图所示,甲、乙两种粗糙面不同但高度相同的传送带,倾斜于水平地面放置。以同样恒定速率v向上运动。现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到传送带的速率v;在乙传送带上到达离B竖直高度为h的C处时达到传送带的速率v。已知B处离地面高度为H,则在物体从A到B的运动过程中( )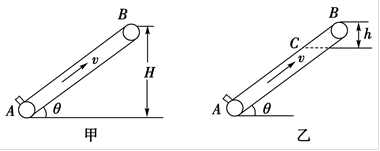
| A.两种传送带对小物体做功相等 |
| B.将小物体传送到B处,两种传送带消耗的电能相等 |
| C.两种传送带与小物体之间的动摩擦因数甲的大 |
| D.将小物体传送到B处,两种系统产生的热量相等 |
质量为2×103 kg,发动机额定功率为80 kW的汽车在平直公路上行驶;若汽车所受阻力大小恒为4×103 N,则下列判断中正确的有
| A.汽车的最大动能是4×105 J |
| B.汽车以加速度2 m/s2匀加速启动,启动后第2秒末时发动机实际功率是32 kW |
| C.汽车以加速度2 m/s2做初速度为0的匀加速运动中,达到最大速度时摩擦力做功为4×105 J |
| D.若汽车保持额定功率启动,则当汽车速度为5 m/s时,其加速度为6 m/s2 |