题目内容
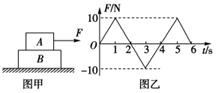
一轻质弹簧一端固定在竖直墙壁上,另一自由端位于O点,现用一滑块将弹簧的自由端(与滑块未拴接)从O点压缩至A点后由静止释放,运动到B点停止,如图甲所示,滑块自A运动到B的v-t图象可能是图乙中的( )
D
解析试题分析:在v-t图象中,图线的斜率表示了物体运动的加速度,滑块由A处释放瞬间,受弹簧向右的推力F和地面的向左的滑动摩擦力f作用,将向右做加速运动,弹簧的压缩量逐渐减小,即推力F逐渐减小,根据牛顿第二定律可知,滑块将先向右做加速度逐渐减小的加速运动,故选项A、B错误;当推力F减小到等于滑动摩擦力f时,滑块的加速度减小至零,此时获得了向右运动的最大速度,此后推力F继续减小,因此滑块将做加速度逐渐增大的减速运动,当滑块运动至O点时,弹簧恢复原长,又由于滑块与弹簧未拴接,因此滑过O点后弹簧与滑块分离,滑块仅在滑动摩擦力f的作用下做匀减速直线运动,故选项C错误;选项D正确。
考点:本题主要考查了物体的受力分析、牛顿第二定律的瞬时性,以及对v-t图象的理解与应用问题,属于中档题。

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案 如图所示,一辆有动力驱动的小车上有一水平放置的弹簧,其左端固定在小车上,右端与一小球相连,设在某一段时间内小球与小车相对静止且弹簧处于压缩状态,若忽略小球与小车间的摩擦力,则在此段时间内小车可能是 ( )
| A.向右做加速运动 | B.向右做减速运动 |
| C.向左做加速运动 | D.向左做减速运动 |
如图所示,劲度系数为k的轻弹簧竖直固定在水平面上,上端固定一质量为m0的托盘,托盘上有一个质量为m的木块。用竖直向下的力将原长为Lo的弹簧压缩后突然撤去外力,则物体m即将脱离m0时的弹簧长度为 ( )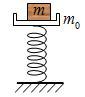
| A.Lo | B.Lo-(m0+m)g/k |
| C.Lo-mg/k | D.Lo-m0g/k |
物体以v0的初速度从倾角为30°的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时,其动能减少了ΔEk=12J,机械能减少了ΔE=2J,不计空气阻力,重力加速度g=10m/s2,则物体沿斜坡向下运动时加速度大小为
| A.2m/s2 | B.3m/s2 | C.4m/s2 | D.6m/s2 |
用力将重物竖直提起,先由静止开始匀加速上升,紧接着匀速上升。如果前后两过程的运动时间相同,不计空气阻力,则( )
| A.加速过程中拉力做的功比匀速过程中拉力做的功多 |
| B.匀速过程中拉力做的功比加速过程中拉力做的功多 |
| C.两过程中拉力做的功一样多 |
| D.上述三种情况都有可能 |
如图所示为阿特伍德设计的装置,不考虑绳与滑轮的质量,不计轴承摩擦、绳与滑轮间的摩擦。初始时两人均站在水平地面上;当位于左侧的甲用力向上攀爬时,位于右侧的乙始终用力抓住绳子,最终至少一人能到达滑轮。下列说法正确的是
| A.若甲的质量较大,则乙先到达滑轮 |
| B.若甲的质量较大,则甲、乙同时到达滑轮 |
| C.若甲、乙质量相同,则乙先到达滑轮 |
| D.若甲、乙质量相同,则甲先到达滑轮 |
如图所示,质量为m的物块,沿着半径为R的半球形金属壳内壁滑下,半球形金属壳竖直固定放置,开口向上,滑到最低点时速度大小为v,若物体与球壳之间的摩擦因数为μ,则物体在最低点时,下列说法正确的是( )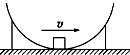
A.受到向心力为mg+m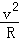 |
B.受到的摩擦力为μm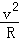 |
C.受到的摩擦力为μ(mg+m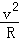 ) ) |
| D.受到的合力方向斜向左上方 |