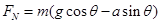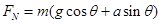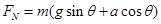题目内容
如图所示，在倾角为α的固定光滑斜面上，有一用绳子拴着的长木板，木板上站着一只猫．已知木板的质量是猫的质量的2倍．当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变．则此时木板沿斜面下滑的加速度为 ( )
A．sin | B． | C．gsin | D．2gsin |
B
解析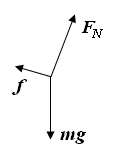
试题分析：对猫受力分析，如图所示，猫保持其相对斜面的位置不变，受到的合力为零，猫受到的摩擦力：f1=mgsinα，方向沿斜面向上，所以木板受到猫施加的沿斜面向下的摩擦力：f2=f1=mgsinα.对木板受力分析，在沿斜面方向上的力有两个：一是它的重力的沿斜面的分力2mgsinα，另一个是沿斜面向下的摩擦力（猫给它），即和它的重力的分力的方向相同，其合力F=f2+2mgsinα=3mgsinα=2ma，所以木板下滑的加速度a=3gsinα/2，故只有B选项正确。
考点：受力分析物体平衡牛顿第二定律
鸿图图书寒假作业假期作业吉林大学出版社系列答案如图所示，某同学用硬塑料管和一个质量为m的铁质螺丝帽研究匀速圆周运动，将螺丝帽套在塑料管上，手握塑料管使其保持竖直并在水平方向做半径为r的匀速圆周运动，则只要运动角速度合适，螺丝帽恰好不下滑，假设螺丝帽与塑料管间的动摩擦因数为μ，认为最大静摩擦力近似等于滑动摩擦力．则在该同学手转塑料管使螺丝帽恰好不下滑时，下述分析正确的是（ ）
| A．螺丝帽受到杆的弹力方向水平向外，背离圆心 |
B．此时手转动塑料管的角速度ω＝ |
| C．螺丝帽受的重力与最大静摩擦力平衡 |
| D．若杆的转动加快，螺丝帽有可能相对杆发生运动 |
和
和如图所示，两个半径相同的半圆形光滑轨道置于竖直平面内，左右两端点等高，分别处于沿水平方向的匀强电场和匀强磁场中.两个相同的带正电小球同时从两轨道左端最高点由静止释放.M、N为轨道的最低点，则下列说法中正确的是（ ）
| A．两个小球到达轨道最低点的速度vM<vN |
| B．两个小球第一次经过轨道最低点时对轨道的压力FM>FN |
| C．小球第一次到达M点的时间大于小球第一次到达N点的时间 |
| D．在磁场中小球能到达轨道的另一端最高处，在电场中小球不能到达轨道另一端最高处 |
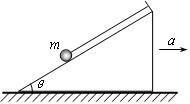
如图所示，足够长的水平传送带A B以
的速度匀速向右运动，另有一物体从传送带的右端向左以
的速度滑上传送带，水平面光滑，传送带表面粗糙，以下说法正确的是
A．若 ，物体回到B点的速度 |
B．若，物体回到B点的速度 |
C．若 ，物体回到B点的速度 |
D．若，物体回到B点的速度 |
物体以v0的初速度从倾角为30°的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时，其动能减少了ΔEk=12J，机械能减少了ΔE=2J，不计空气阻力，重力加速度g=10m/s2，则物体沿斜坡向下运动时加速度大小为
| A．2m/s2 | B．3m/s2 | C．4m/s2 | D．6m/s2 |
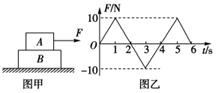
如图所示，在光滑水平面上叠放着甲、乙两物体。现对甲施加水平向右的拉力F，通过传感器可测得甲的加速度a随拉力F变化的关系如图所示。巳知重力加速度g="10" m/s2，由图线可知（ ）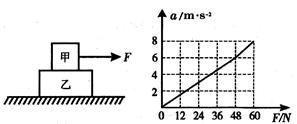
| A．甲的质量是2kg |
| B．甲的质量是6kg |
| C．甲、乙之间的动摩擦因数是0.2 |
| D．甲、乙之间的动摩擦因数是0.6 |