题目内容
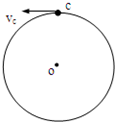
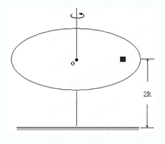
一半径为
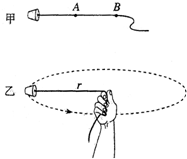
R圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动,圆盘距地面的竖直高度为2R,距圆盘中心R处放一小木块,它与圆盘之间相对静止且随圆盘一起做匀速圆周运动,已知木块与圆盘之间的动摩擦因数为
.设木块与圆盘间的最大静摩擦力等于滑动摩擦力.
(1)求圆盘转动的最大角速度;
(2)若圆盘以最大角速度转动,某时刻圆盘突然停止转动,小木块离开圆盘最后落到地面.求木块离开圆盘时的速度大小及落地点与圆盘中心O的水平距离.
| ||
| 8 |
| 1 |
| 3 |
(1)求圆盘转动的最大角速度;
(2)若圆盘以最大角速度转动,某时刻圆盘突然停止转动,小木块离开圆盘最后落到地面.求木块离开圆盘时的速度大小及落地点与圆盘中心O的水平距离.

(1)当小木块受到的静摩擦力达到最大时,角速度最大,根据向心力公式得:
μmg=mω2R
解得:ω=
=
(2)停止转动后,小木块先沿切线方向做匀减速直线运动,根据牛顿第二定律得:
a=
=-μg
根据v2-v02=2as
其中s=
=
得:v0=ωR=
综上述四式得:v=
离开圆盘后做平抛运动,平抛运动的时间为:t=
=2
水平射程为:x=vt=R
根据几何关系,距O点的水平距离为:x′=
=
R
答:(1)圆盘转动的最大角速度为
;
(2)木块离开圆盘时的速度大小为
,落地点与圆盘中心O的水平距离为
R.
μmg=mω2R
解得:ω=
|
|
(2)停止转动后,小木块先沿切线方向做匀减速直线运动,根据牛顿第二定律得:
a=
| -μmg |
| m |
根据v2-v02=2as
其中s=
(
|
| R |
| 8 |
得:v0=ωR=
|
综上述四式得:v=
| ||
| 2 |
离开圆盘后做平抛运动,平抛运动的时间为:t=
|
|
水平射程为:x=vt=R
根据几何关系,距O点的水平距离为:x′=
(
|
| ||
| 8 |
答:(1)圆盘转动的最大角速度为
|
(2)木块离开圆盘时的速度大小为
| ||
| 2 |
| ||
| 8 |

练习册系列答案
相关题目