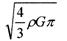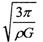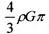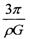题目内容
在发射地球同步卫星的过程中,卫星首先进入椭圆轨道Ⅰ,然后在Q点通过改变卫星速度,让卫星进入地球同步轨道Ⅱ。若卫星的发射速度为v0,第一宇宙速度为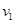 ,在同步轨道Ⅱ上的运行速度为
,在同步轨道Ⅱ上的运行速度为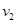 ,则
,则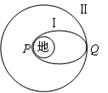
A.v0>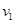 > >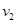 |
| B.若卫星的发射速度为2v0,卫星最终围绕地球运行的轨道半径将变大。 |
| C.在轨道Ⅰ上,卫星在P点的速度等于在Q点的速度 |
| D.卫星在Q点通过加速实现由轨道Ⅰ进入轨道Ⅱ |
AD
解析试题分析:7.9km/s即第一宇宙速度是发射卫星的最小速度,也是最大的圆周运动的环绕速度,而同步卫星的轨道半径要大于近地卫星的轨道半径,根据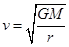 可以发现,同步卫星运行的线速度一定小于第一宇宙速度,故v0>v1>v2,所以A正确;若卫星的发射速度为2v0,即大于11.2km/s,将脱离地球,所以B错误;卫星首先进入椭圆轨道Ⅰ,在轨道Ⅰ上,由P点向Q点运动,万有引力做负功,动能减小,所以P点的速度大于Q点的速度,故C错误;从椭圆轨道Ⅰ到同步轨道Ⅱ,卫星在Q点是做逐渐远离圆心的运动,要实现这个运动必须卫星所需向心力大于万有引力,所以应给卫星加速,增加所需的向心力.所以在轨道Ⅱ上Q点的速度大于轨道上Ⅰ经过Q点的速度.故D正确
可以发现,同步卫星运行的线速度一定小于第一宇宙速度,故v0>v1>v2,所以A正确;若卫星的发射速度为2v0,即大于11.2km/s,将脱离地球,所以B错误;卫星首先进入椭圆轨道Ⅰ,在轨道Ⅰ上,由P点向Q点运动,万有引力做负功,动能减小,所以P点的速度大于Q点的速度,故C错误;从椭圆轨道Ⅰ到同步轨道Ⅱ,卫星在Q点是做逐渐远离圆心的运动,要实现这个运动必须卫星所需向心力大于万有引力,所以应给卫星加速,增加所需的向心力.所以在轨道Ⅱ上Q点的速度大于轨道上Ⅰ经过Q点的速度.故D正确
考点:本题考查天体运动,涉及发射速度、宇宙速度、环绕速度计卫星变轨问题,意在考查学生的综合分析能力。

太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度大小约为地球绕太阳公转速度的7倍,其轨道半径约为地球绕太阳公转轨道半径的2×109倍。为了粗略估算银河系中恒星的数目,可认为银河系的所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳的质量,则银河系中恒星的数目约为( )
| A.1015 | B.1013 | C.1011 | D.109 |
通常我们把太阳系中行星自转一周的时间称为“1天”,绕太阳公转一周的时间称为“1年”,已知金星的“1天”比它的“1年”还长。与地球相比较,金星的“1天”的时间约是地球 “1天”的时间的243倍。由此可知( )
| A.地球自转角速度约是金星自转角速度的243倍 |
| B.金星的质量约是地球质量的243倍 |
| C.金星的半径约是地球半径的243倍 |
| D.地球表面重力加速度约是金星表面的重力加速度的243倍 |
课堂上老师给同学们布置了这样一个题目:假设地球是一半径为R,质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。李明同学的思考过程如下: 由等式GM=gR2(G为引力常量,M为地球质量,R为地球半径,g为地球表面处的重力加速度)变形后得到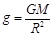 ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比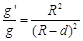 。下列说法中正确的是
。下列说法中正确的是
| A.李明的答案是正确的 |
| B.李明的答案是错误的,因为等式GM=gR2不成立 |
| C.李明的答案是错误的,因为本题不能用等式GM=gR2求解 |
| D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误 |
两颗人造地球卫星,质量之比m1:m2=1:2,轨道半径之比R1:R2=3:1,下面有关数据之比正确的是( )
| A.周期之比T1:T2=3:1 |
| B.线速度之比v1:v2=3:1 |
| C.向心力之比为F1:F2=1:9 |
| D.向心加速度之比a1:a2=1:9 |
2010年10月1日,“嫦娥二号”在西昌卫星基地发射成功,其环月飞行的高度距离月球表面100 km,所探测到的有关月球的数据将比环月飞行高度为200 km的“嫦娥一号”更加详实.若两颗卫星环月运行均可视为匀速圆周运动,运行轨道如图8所示,则( ).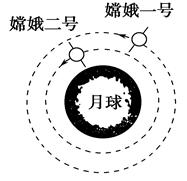
| A.“嫦娥二号”环月运行的速度比“嫦娥一号”更小 |
| B.“嫦娥二号”环月运行时向心加速度比“嫦娥一号”更小 |
| C.“嫦娥二号”环月运行的周期比“嫦娥一号”更小 |
| D.“嫦娥二号”环月运行时角速度与“嫦娥一号”相等 |





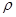 ,若由于星球自转使物体对星球表面的压力恰好为零,则星球自转的角速度为
,若由于星球自转使物体对星球表面的压力恰好为零,则星球自转的角速度为