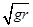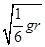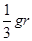题目内容
如图所示,a为地球赤道上的物体,b为沿地球表面附近做匀速圆周运动的人造卫星,c为地球同步卫星.关于a、b、c做匀速圆周运动的说法中正确的是( )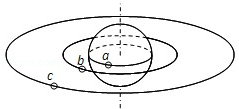
| A.角速度的大小关系为ωa=ωc>ωb | B.向心加速度的大小关系为aa>ab>ac |
| C.线速度的大小关系为va>vb>vc | D.周期关系为Ta=Tc>Tb |
D
解析试题分析:a、c角速度相等,根据a=ω2r判断向心加速度大小,根据v=ωr判断线速度大小;b、c都是卫星,根据万有引力提供向心力判断加速度和线速度大小.
A、a、c角速度相等,即ωa=ωc,而rb<rc,根据ω=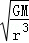 可知:ωc<ωb,所以ωa=ωc<ωb,故A错误;
可知:ωc<ωb,所以ωa=ωc<ωb,故A错误;
B、由a=ω2r,得:aa<aC,故B错误;
C、AC比较,角速度相等,由v=ωr,可知υa<υc,故C错误;
D、卫星C为同步卫星,所以Ta=Tc,根据T=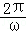 及ωc<ωb,可知Tc>Tb,所以Ta=Tc>Tb,故D正确;
及ωc<ωb,可知Tc>Tb,所以Ta=Tc>Tb,故D正确;
故选D.
考点:人造卫星的加速度、周期和轨道的关系;万有引力定律及其应用
点评:本题涉及到两种物理模型,即AC转动的周期相等,BC同为卫星,其动力学原理相同,要两两分开比较,最后再统一比较

将卫星发射至近地圆轨道1,然后再次点火,将卫星送入同步轨道3。轨道1、2相切于 点,2、3相切于
点,2、3相切于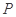 点,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
点,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )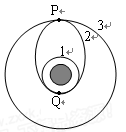
| A.卫星在轨道3上的周期大于轨道1上的周期 |
| B.卫星在轨道3上的速率大于在轨道1上的速率 |
C.卫星在轨道1上经过 点时的速率小于它在轨道2上经过Q点时的速率 点时的速率小于它在轨道2上经过Q点时的速率 |
| D.无论卫星在2轨道还是3轨道,卫星在P点加速度相等 |
假设太阳系中天体的密度不变,天体直径和天体之间距离都缩小到原来的一半,地球绕太阳公转近似为匀速圆周运动,则下列物理量变化正确的是( )
| A.地球的向心力变为缩小前的一半 |
B.地球的向心力变为缩小前的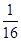 |
| C.地球绕太阳公转周期与缩小前的相同 |
| D.地球绕太阳公转周期变为缩小前的一半 |
太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度大小约为地球绕太阳公转速度的7倍,其轨道半径约为地球绕太阳公转轨道半径的2×109倍。为了粗略估算银河系中恒星的数目,可认为银河系的所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳的质量,则银河系中恒星的数目约为( )
| A.1015 | B.1013 | C.1011 | D.109 |
两颗人造地球卫星,质量之比m1:m2=1:2,轨道半径之比R1:R2=3:1,下面有关数据之比正确的是( )
| A.周期之比T1:T2=3:1 |
| B.线速度之比v1:v2=3:1 |
| C.向心力之比为F1:F2=1:9 |
| D.向心加速度之比a1:a2=1:9 |
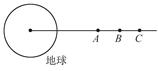
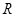 约45km,质量
约45km,质量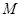 和半径
和半径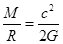 (其中
(其中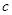 为光速,
为光速,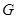 为引力常量),则该黑洞表面重力加速度的数量级为 ( )
为引力常量),则该黑洞表面重力加速度的数量级为 ( )
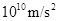
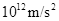
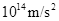
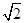 v1.已知某星球的半径为r,表面的重力加速度为地球表面重力加速度g的1/6,不计其它星球的影响,则该星球的第二宇宙速度为
v1.已知某星球的半径为r,表面的重力加速度为地球表面重力加速度g的1/6,不计其它星球的影响,则该星球的第二宇宙速度为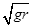
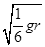

 gr
gr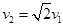 。已知某星球的半径为r,它表面的重力加速度为地球表面重力加速度g的1/6,不计其他星球的影响,则该星球的第二宇宙速度为
。已知某星球的半径为r,它表面的重力加速度为地球表面重力加速度g的1/6,不计其他星球的影响,则该星球的第二宇宙速度为