题目内容
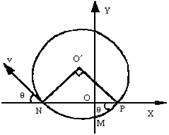
如下图所示,在直角坐标系的第一、二象限内有垂直于纸面的勾强磁场,第三象限有沿Y轴负方向的匀强电场,第四象限内无电场和磁场.质量为m、带电量为q的粒子从M点以速度v0沿X轴负方向进入电场,不计粒子的重力,粒子经N、和X轴上的P点最后又回到M点.设OM=OP=l,ON=2l,求:

(1)电场强度E的大小.
(2)匀强磁场的磁感强度B的大小和方向.
(3)粒子从M点进入电场,经N、P点最后又回到M点所用的时间.

(1)电场强度E的大小.
(2)匀强磁场的磁感强度B的大小和方向.
(3)粒子从M点进入电场,经N、P点最后又回到M点所用的时间.
(1)
 (2)
(2) 方向垂直纸面向里
方向垂直纸面向里(3) (3+
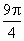 )
)
(1)根据粒子在电场中运动的情况可知,粒子带负电,粒子在电场中运动所用的时间设为t1,X方向:2l=v0t1
Y方向:l= ·
· t12
t12
解得:电场强度E=
(2)设到达N点的速度为v,运动方向与一X轴方向的夹角为θ,如图所示
由动能定理得qEl= mv2-
mv2- mv02
mv02
将E= 代入得v=
代入得v= v0
v0
∵cosθ= ∴θ=
∴θ=
粒子在磁场中做匀速圆周运动,经过P点时速度方向也与一X方向成 ,从P到M作直线运动 OP=OM=l NP=NO+OP=3l
,从P到M作直线运动 OP=OM=l NP=NO+OP=3l
粒子在磁场中的轨道半径为
R=NP· =
= l 又因R=
l 又因R=
联立解得 B= 方向垂直纸面向里
方向垂直纸面向里
(3)粒子在电场中运动的时间为t1,t1=
设粒子在磁场中运动所用的时间为t2,有t2= T=
T= ·
· =
=
从p离开磁场作匀速直线运动到M所用的时间为t3,t3= =
=
粒子从M点进入电场,经N、P点最后又回到M点所用的时间为:
t=t1+t2+t3=(3+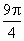 )
)

Y方向:l=
 ·
· t12
t12解得:电场强度E=

(2)设到达N点的速度为v,运动方向与一X轴方向的夹角为θ,如图所示
由动能定理得qEl=
 mv2-
mv2- mv02
mv02将E=
 代入得v=
代入得v= v0
v0∵cosθ=
 ∴θ=
∴θ=
粒子在磁场中做匀速圆周运动,经过P点时速度方向也与一X方向成
 ,从P到M作直线运动 OP=OM=l NP=NO+OP=3l
,从P到M作直线运动 OP=OM=l NP=NO+OP=3l粒子在磁场中的轨道半径为
R=NP·
 =
= l 又因R=
l 又因R=
联立解得 B=
 方向垂直纸面向里
方向垂直纸面向里(3)粒子在电场中运动的时间为t1,t1=

设粒子在磁场中运动所用的时间为t2,有t2=
 T=
T= ·
· =
=
从p离开磁场作匀速直线运动到M所用的时间为t3,t3=
 =
=
粒子从M点进入电场,经N、P点最后又回到M点所用的时间为:
t=t1+t2+t3=(3+
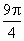 )
)

练习册系列答案
相关题目
 f = 0.1mg, PN =
f = 0.1mg, PN = ,取g =10m/s2。a、b均可作为质点。(结果保留三位有效数字)求:
,取g =10m/s2。a、b均可作为质点。(结果保留三位有效数字)求:





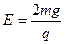
 ,则小环在两根直轨道上通过的总路程多大?
,则小环在两根直轨道上通过的总路程多大?