题目内容
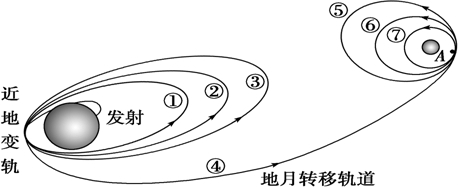
2007年10月24日18时,“嫦娥一号”卫星星箭成功分离,卫星进入绕地轨道.在绕地运行时,要经过三次近地变轨:12小时椭圆轨道①→24小时椭圆轨道②→48小时椭圆轨道③→地月转移轨道④.11月5日11时,当卫星经过距月球表面高度为h的A点时,再一次实施变轨,进入12小时椭圆轨道⑤,后又经过两次变轨,最后进入周期为T的月球极月圆轨道⑦.如图所示.已知月球半径为R.
(1)请回答:“嫦娥一号”在完成三次近地变轨时需要加速还是减速?
(2)写出月球表面重力加速度的表达式.
(1)请回答:“嫦娥一号”在完成三次近地变轨时需要加速还是减速?
(2)写出月球表面重力加速度的表达式.

(1)在完成三次近地变轨时,椭圆的半长轴越来越大,知在近地变轨时,速度变大,做半长轴更大的离心运动,故物体做加速运动;
(2)设月球表面的重力加速度为g月,根据万有引力等于重力,在月球表面有G
=mg月
根据万有引力提供向心力,卫星在极月圆轨道有
=m(
)2(R+h)
联立两式解得g月=
.
答:(1)加速
(2)月球表面重力加速度的表达式
.
(2)设月球表面的重力加速度为g月,根据万有引力等于重力,在月球表面有G
| Mm |
| R2 |
根据万有引力提供向心力,卫星在极月圆轨道有
| GMm |
| (R+h)2 |
| 2π |
| T |
联立两式解得g月=
| 4π2(R+h)3 |
| T2R2 |
答:(1)加速
(2)月球表面重力加速度的表达式
| 4π2(R+h)3 |
| T2R2 |

练习册系列答案
相关题目