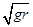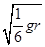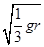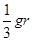题目内容
为了探测X星球,载着登陆舱的探测飞船在以该星球中心为圆心,半径为r1的圆轨道上运动,周期为T1.总质量为m1.随后登陆舱脱离飞船,变轨到离星球更近的半径为r2的圆轨道上运动,此时登陆舱的质量为m2则( )
A.X星球的质量为 |
B.X星球表面的重力加速度为 |
C.登陆舱在r1与r2轨道上运动时的速度大小之比为 |
D.登陆舱在半径为r2轨道上做圆周运动的周期为 |
AD
解析试题分析:研究飞船绕星球做匀速圆周运动,根据万有引力提供向心力,列出等式求出中心体的质量.
研究登陆舱绕星球做匀速圆周运动,根据万有引力提供向心力,列出等式表示出线速度和周期.再通过不同的轨道半径进行比较.
A、研究飞船绕星球做匀速圆周运动,根据万有引力提供向心力,列出等式: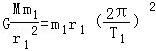
得出:M=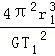 ,故A正确.
,故A正确.
B、根据圆周运动知识,a=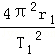 只能表示在半径为r1的圆轨道上向心加速度,而不等于X星球表面的重力加速度,故B错误.
只能表示在半径为r1的圆轨道上向心加速度,而不等于X星球表面的重力加速度,故B错误.
C、研究登陆舱绕星球做匀速圆周运动,根据万有引力提供向心力有:
在半径为r的圆轨道上运动: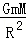 =m
=m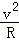 得出:v=
得出:v=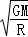 ,表达式里M为中心体星球的质量,R为运动的轨道半径.
,表达式里M为中心体星球的质量,R为运动的轨道半径.
所以登陆舱在r1与r2轨道上运动时的速度大小之比为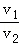 =
=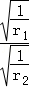 =
=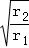 ,故C错误.
,故C错误.
D、研究登陆舱绕星球做匀速圆周运动,根据万有引力提供向心力,列出等式:
在半径为r的圆轨道上运动: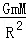 =m
=m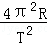 得出:T=2π
得出:T=2π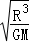 .表达式里M为中心体星球的质量,R为运动的轨道半径.所以登陆舱在r1与r2轨道上运动时的周期大小之比为:
.表达式里M为中心体星球的质量,R为运动的轨道半径.所以登陆舱在r1与r2轨道上运动时的周期大小之比为: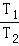 =
= ,所以T2=T1
,所以T2=T1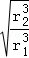 ,故D正确.
,故D正确.
故选AD.
考点:万有引力定律及其应用
点评:求一个物理量之比,我们应该把这个物理量先用已知的物理量表示出来,再进行之比.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

“嫦娥二号”探月卫星于2010年10月1日成功发射,目前正在月球上方100km的圆形轨道上运行。已知“嫦娥二号”卫星的运行周期、月球半径、月球表面重力加速度、万有引力恒量G。根据以上信息可求出
| A.卫星所在处的加速度 | B.月球的平均密度 |
| C.卫星线速度大小 | D.卫星所需向心力 |
假设太阳系中天体的密度不变,天体直径和天体之间距离都缩小到原来的一半,地球绕太阳公转近似为匀速圆周运动,则下列物理量变化正确的是( )
| A.地球的向心力变为缩小前的一半 |
B.地球的向心力变为缩小前的 |
| C.地球绕太阳公转周期与缩小前的相同 |
| D.地球绕太阳公转周期变为缩小前的一半 |
某星球与地球的质量比为a,半径比为b,则该行星表面的重力加速度与地球表面重力加速度之比为
| A.a/b | B.a/b2 | C.ab2 | D.ab |
课堂上老师给同学们布置了这样一个题目:假设地球是一半径为R,质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。李明同学的思考过程如下: 由等式GM=gR2(G为引力常量,M为地球质量,R为地球半径,g为地球表面处的重力加速度)变形后得到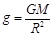 ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比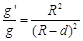 。下列说法中正确的是
。下列说法中正确的是
| A.李明的答案是正确的 |
| B.李明的答案是错误的,因为等式GM=gR2不成立 |
| C.李明的答案是错误的,因为本题不能用等式GM=gR2求解 |
| D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误 |
 。已知地球半径为
。已知地球半径为 ,地球质量为
,地球质量为 ,引力常量为
,引力常量为 。关于弹头在C点的速度
。关于弹头在C点的速度 和加速度
和加速度 ,正确的是 ( )
,正确的是 ( ) 

 B.
B.
 D.
D.

 约45km,质量
约45km,质量 和半径
和半径 (其中
(其中 为光速,
为光速, 为引力常量),则该黑洞表面重力加速度的数量级为 ( )
为引力常量),则该黑洞表面重力加速度的数量级为 ( )



 。已知某星球的半径为r,它表面的重力加速度为地球表面重力加速度g的1/6,不计其他星球的影响,则该星球的第二宇宙速度为
。已知某星球的半径为r,它表面的重力加速度为地球表面重力加速度g的1/6,不计其他星球的影响,则该星球的第二宇宙速度为