题目内容
“嫦娥二号”探月卫星于2010年10月1日成功发射,目前正在月球上方100km的圆形轨道上运行。已知“嫦娥二号”卫星的运行周期、月球半径、月球表面重力加速度、万有引力恒量G。根据以上信息可求出
| A.卫星所在处的加速度 | B.月球的平均密度 |
| C.卫星线速度大小 | D.卫星所需向心力 |
ABC
解析试题分析:根据 ,可以计算得到月球的质量M,再根据体积可以计算月球的密度,B正确;再根据
,可以计算得到月球的质量M,再根据体积可以计算月球的密度,B正确;再根据  可以计算得到卫星所在处的加速度,A正确;根据
可以计算得到卫星所在处的加速度,A正确;根据 计算卫星线速度大小,C正确;由于不知道卫星的的质量,不能计算卫星所需向心力,D错误。
计算卫星线速度大小,C正确;由于不知道卫星的的质量,不能计算卫星所需向心力,D错误。
考点:本题考查了万有引力与卫星问题。

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案设想我国宇航员随“嫦娥”号登月飞船贴近月球表面做匀速圆周运动,宇航员测出飞船绕行n圈所用的时间为t。登月后,宇航员利用身边的弹簧秤测出质量为m的物体重力G1。已知引力常量为G,根据以上信息可得到 ( )
| A.月球的密度 | B.飞船的质量 |
| C.月球的第一宇宙速度 | D.月球的自转周期 |
目前,在地球周围有许多人造地球卫星绕着它运转,其中一些卫星的轨道可近似为圆,且轨道半径逐渐变小。若卫星在轨道半径逐渐变小的过程中,只受到地球引力和稀薄气体阻力的作用,则下列判断正确的是
| A.由于气体阻力做负功,卫星的动能逐渐减小 |
| B.由于地球引力做正功,引力势能一定减小 |
| C.由于气体阻力做功可忽略,因此机械能保持不变 |
| D.卫星克服气体阻力做的功等于引力势能的减小 |
据悉,我省女宇航员王亚平搭乘“神舟十号”飞船于2013年6月上旬飞向太空,“神舟十号”发射初始轨道为近地点约200公里、远地点约330公里的椭圆轨道,升空后再和目标飞行器“天宫一号”对接,并对其进行短暂的有人照管试验,交会对接轨道为距地约343公里的近圆轨道。假设“神舟十号”飞船发射升空后,先后经历了多次变轨·调整到处于“天宫一号”目标飞行器后方约52km处,并与“天宫一号”处于同一离地面高度相同的圆形轨道上,最后与“天宫一号”实施对接,完成浪漫的“太空之吻”。忽略它们之间的万有引力,则
| A.“神舟十号”与“天宫一号”受到地球吸引力的大小相等 |
| B.“神舟十号”由初始椭圆轨道变为最终的圆形轨道时周期变长 |
| C.“天宫一号”的速度比地球同步卫星速度小 |
| D.对接前,“神舟十号”欲追上“天宫一号”,必须在同一轨道上点火加速 |
“嫦娥二号”环月飞行的高度为100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实。若两颗卫星环月的运行均可视为匀速圆周运动,运行轨道如图所示。则
| A.“嫦娥二号”环月运行的周期比“嫦娥一号”大 |
| B.“嫦娥二号”环月运行的线速度比“嫦娥一号”小 |
| C.“嫦娥二号”环月运行的向心加速度比“嫦娥一号”大 |
| D.“嫦娥二号”环月运行的向心力与“嫦娥一号”相等 |
组成星球的物质是靠引力吸引在一起的,这样的星球有一个最大的自转速率.如果超过了该速率,星球的万有引力将不足以维持其赤道附近的物体做圆周运动.由此能得到半径为R、密度为ρ、质量为M且均匀分布的星球的最小自转周期T.下列表达式中正确的是( )
A.T=2π | B.T=2π |
C.T= | D.T= |
为了探测X星球,载着登陆舱的探测飞船在以该星球中心为圆心,半径为r1的圆轨道上运动,周期为T1.总质量为m1.随后登陆舱脱离飞船,变轨到离星球更近的半径为r2的圆轨道上运动,此时登陆舱的质量为m2则( )
A.X星球的质量为 |
B.X星球表面的重力加速度为 |
C.登陆舱在r1与r2轨道上运动时的速度大小之比为 |
D.登陆舱在半径为r2轨道上做圆周运动的周期为 |
 做匀速圆周运动,轨道半径为
做匀速圆周运动,轨道半径为 ,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如题2图所示.若卫星均沿顺时针方向运行,地球表面的重力加速度为
,某时刻两颗工作卫星分别位于轨道上的A、B两位置,如题2图所示.若卫星均沿顺时针方向运行,地球表面的重力加速度为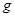 ,地球半径为
,地球半径为 ,
, ,下述说法中正确的是
,下述说法中正确的是


 ,半径为
,半径为 ,自转角速度为
,自转角速度为 ,万有引力常量为
,万有引力常量为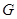 ,同步卫星离地心高度为
,同步卫星离地心高度为 ,地表重力加速度为
,地表重力加速度为 ,则同步卫星的速度
,则同步卫星的速度 :①
:① ;②
;② ;③
;③ ;④
;④ .其中正确的是( )
.其中正确的是( )