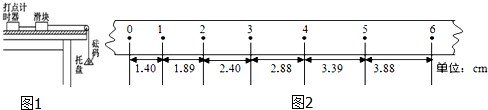
题目内容
2.某研究小组设计了一种“用一把尺子测定动摩擦因数”的实验方案.如图所示,A是可固定于水平桌面上任意位置的滑槽(滑槽末端与桌面相切),B是质量为m的滑块(可视为质点).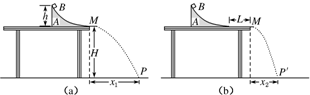
第一次实验,如图(a)所示,将滑槽末端与桌面右端M对齐并固定,让滑块从滑槽最高点由静止滑下,最终落在水平地面上的P点,测出滑槽最高点距离桌面的高度h、M距离地面的高度H、M与P间的水平距离x1;
第二次实验,如图(b)所示,将滑槽沿桌面向左移动一段距离并固定,让滑块B再次从滑槽最高点由静止滑下,最终落在水平地面上的P′点,测出滑槽末端与桌面右端M的距离L、M与P′间的水平距离x2.
(1)在第二次实验中,滑块在滑槽末端时的速度大小为${x}_{2}\sqrt{\frac{g}{2H}}$.(用实验中所测物理量的符号表示,已知重力加速度为g).
(2)(多选)通过上述测量和进一步的计算,可求出滑块与桌面间的动摩擦因数μ,下列能引起实验误差的是BCD
A.h的测量 B.H的测量 C.L的测量 D.x2的测量
(3)若实验中测得h=15cm、H=25cm、x1=30cm、L=10cm、x2=20cm,则滑块与桌面间的动摩擦因数μ=0.5.
分析 (1)由平抛运动的知识求得速度的大小.
(2)凡影响到速度大小的求解的量均会引起实验误差.
(3)先列出μ的表达式,代入数据计算即可.
解答 解:(1)由平抛运动知:设滑块在滑槽末端时的速度大小为v1,由水平方向的匀速直线运动,有:x1=v1t,
由竖直方向的自由落体运动H=$\frac{1}{2}$gt2,解得:v1=x1$\sqrt{\frac{g}{2H}}$.
(2)同理滑块第一次测在滑槽末端时的速度大小为:v1=x1$\sqrt{\frac{g}{2H}}$,第二次在桌面右端M 点的速度大小为:v2=x2$\sqrt{\frac{g}{2H}}$,物体在水平桌面上运动,
由动能定理:-μmgL=$\frac{1}{2}$m${v}_{2}^{2}$-$\frac{1}{2}$m${v}_{1}^{2}$可得:μ=$\frac{{x}_{1}^{2}{-x}_{2}^{2}}{4HL}$,由表达式可知会引起误差的是选项BCD.
(3)H=25cm=0.25m、x1=30cm=0.30m、L=10cm=0.10m、x2=20cm=0.20m
由(2)问中的μ的表达式μ=$\frac{{x}_{1}^{2}{-x}_{2}^{2}}{4HL}$可求得:μ=0.5.
故答案为:(1)${x}_{2}\sqrt{\frac{g}{2H}}$;(2)BCD;(3)0.5
点评 该实验有一定的创新性,其实很多复杂的实验其实验原理都是来自我们所学的基本规律,这点要在平时训练中去体会

练习册系列答案
相关题目
20.关于电阻和电阻率,下列说法中正确的是( )
| A. | 由R=$\frac{U}{I}$可知,电阻与电压、电流都有关系 | |
| B. | 由ρ=$\frac{RS}{l}$可知,ρ与R、S成正比,ρ与l成反比 | |
| C. | 材料的电阻率都随温度的升高而增大 | |
| D. | 对某一确定的导体,当温度升高时,发现它的电阻增大,说明该导体材料的电阻率随温度的升高而增大 |
1.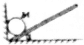 如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
 如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
如图所示,一个质量为M的球靠墙置于水平光滑板上,墙也是光滑的,当平板的一端慢慢抬起,使之与水平方向的夹角由0°变为α,在此过程中,墙受的压力大小的变化情况是变大;平板受到的压力大小变化情况是变大.
18.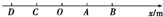 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
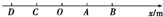 某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )
某一运动质点沿一直线做往返运动,如图所示,OA=AB=OC=CD=1m,O点为x轴上的原点,且质点由A点出发向x轴的正方向运动至B点再返回沿x轴的负方向运动,以下说法正确的是( )| A. | 质点在A→B→C的时间内发生的位移为2 m,方向沿x轴正方向,路程为4 m | |
| B. | 质点在B→D的时间内发生的位移为-4 m,方向沿x轴负方向,路程为4 m | |
| C. | 当质点到达D点时,其位置可用D点的坐标-2 m表示 | |
| D. | 当质点到达D点时,相对于A点的位移为-3 m |
7.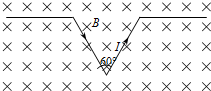 长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )
长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )
 长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )
长为4L的直导线等分成四等份,拆成如图所示的图形,其中的V形导线夹角为60°,整个图形置于与其所在平面相垂直的匀强磁场中,磁场的磁感应强度为B,当在该导线中通以大小为I的电流时,该V形通电导线受到的安培力大小为( )| A. | BIL | B. | 2BIL | C. | 3BIL | D. | 4BIL |
14.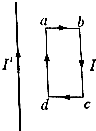 长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
 长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )
长方形线框abcd通有恒定电流I,在线框所在平面内线框的左侧与ad边平行放置一长直导线,导线中通有恒定电流I′,电流的方向如图所示,线框和长直导线的位置都被固定,下列关于线框受到安培力的说法中正确的是( )| A. | 线框的ab和cd边不受安培力 | |
| B. | 线框所受的安培力合力向右 | |
| C. | 线框所受的安培力合力向左 | |
| D. | 若长直导线的电流I′加倍,则稳定后线框所受的安培力合力也随之加倍 |
12.下列说法中哪个说的是时间( )
| A. | 天宫二号于2016年9月15日22时04分09秒点火发射成功 | |
| B. | 中央电视台新闻联播节目每天播放约30min | |
| C. | 中央电视台新闻联播节目每天19:00开播 | |
| D. | 某学校上早自习从6点55开始 |
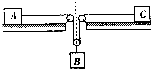 如图所示,半径为R的水平转台中央有一个小孔,水平转台可绕小孔中心轴匀速转动,物块A、C置于转台的边缘,物块A、C的质量均为m,随转台一起转动,用细绳通过大小不计的轻质滑轮悬挂物块B,三物块均可看成质点.已知物块A、C与转台间的动摩擦因数均为μ=0.5,水平转台的角速度ω=$\sqrt{\frac{2μg}{R}}$,重力加速度大小为g.要使物块B静止不动,物块A、B的质量之比可能为( )
如图所示,半径为R的水平转台中央有一个小孔,水平转台可绕小孔中心轴匀速转动,物块A、C置于转台的边缘,物块A、C的质量均为m,随转台一起转动,用细绳通过大小不计的轻质滑轮悬挂物块B,三物块均可看成质点.已知物块A、C与转台间的动摩擦因数均为μ=0.5,水平转台的角速度ω=$\sqrt{\frac{2μg}{R}}$,重力加速度大小为g.要使物块B静止不动,物块A、B的质量之比可能为( )