题目内容
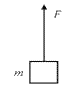
【题目】如图所示,“L”形槽固定在光滑水平面,槽的曲面部分光滑,水平部分粗糙且长度d=2m,上方有水平向右的匀强电场,场强E=102N/C.不带电的绝缘物体B静止在槽的水平部分最左端,在槽的最右端并排放置一个与它等高的,足够长的木板C,足够远处有竖直的挡板P.ABC质量均为m=1kg,现将带正电的电量q=5×10﹣2C,物体A从槽的曲面上距B的竖直高度为h=0.8m处由静止释放,已知A.B与槽的水平部分及C的上表面的动摩擦因数均为μ=0.4.A与B,C与P的碰撞过程时间极短且碰撞过程中无机械能损失.A.B均可看作质点且A的电量始终保持不变,g取10m/s2.求:

(1)A与B第一次碰撞后B的速度;
(2)A与B第二次碰撞后B的速度;
(3)物体B最终停在距离木板C左端多远处.
【答案】(1) 4m/s (2) 2m/s (3) 0.5m
【解析】
(1)A与B第一次碰撞前,由机械能守恒定律得
![]()
解得:v0=4m/s
规定向右为正方向,碰撞过程动量守恒:
mv0=mvA+mvB
机械能守恒:
![]()
解得:vA=0,vB=4m/s
(2)A与B第一次碰撞后A做匀加速直线运动,
加速度大小
![]()
B做匀减速速直线运动,根据牛顿第二定律得
加速度大小
![]()
B的速度减到零所需的时间为
![]()
B的位移
![]()
位移为![]()
而A作匀加速直线运动1s发生的位移为
所以当B的速度减到零以后才发生第二次碰撞,第二次碰撞前A的速度
![]()
由动量守恒定律及机械能守恒可得:
A B第二次碰撞后B获得的速度v'B=2m/s
(3)A与B完成第二次碰撞后A将静止.此时B刚好滑上C的上表面,
B与C在第一次与挡板P碰前的共同速度为
mv'B=2mv1;
代入数据得:v1=1m/s
C与P碰后向左运动,因为B与C动量大小相同,方向相反,取水平向右为正方向,
根据动量守恒定律得
mv1﹣mv1=2mv2
代入数据得:v2=0
最终BC静止,B的动能全部转化为内能,由能量守恒得:
![]()
而Q=μmgs
故B距离C的左端:s=0.5m