题目内容
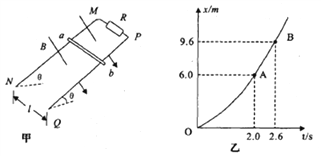
【题目】如图所示,倾斜固定的光滑绝缘细杆上套有一个带正电的小球(可视为点电荷),其质量为m、电荷量为q,杆与水平面的夹角为45°,在杆底端C点的正上方O点处固定放置一电荷量为Q的带正电的点电荷,O点与杆在同一竖直平而内,杆上B点与O在同一水平面内,现让小球在A点由静止释放,到达B点的速度为v,B为AC的中点,A、C间距离为2L,重力加速度为g.求:
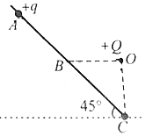
(1)小球到达B点时的加速度;
(2)小球到达C点时的速度.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
根据牛顿第二定律求小球到达B点时的加速度;从B到C根据动能定理求小球到达C点的速度;
解:(1)小球到达B点时,对小球受力分析如图
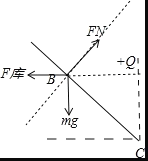
根据牛顿第二定律,有:![]()
解得:![]()
(2)BC两点电势相等![]() ,电场力做功为0
,电场力做功为0
从B到C根据动能定理,有:![]()
解得:![]()

练习册系列答案
相关题目
【题目】一辆汽车从静止开始匀加速开出,然后保持匀速运动,最后匀减速运动,直到停止,下表给出了不同时刻汽车的速度:
时刻/s | 1.0 | 2.0 | 3.0 | 5.0 | 7.0 | 9.5 | 10.5 |
速度/(m·s-1) | 3 | 6 | 9 | 12 | 12 | 9 | 3 |
(1)汽车从开出到停止总共经历的时间是多少?
(2)汽车通过的总路程是多少?