题目内容
8. 如图所示,一个边缘带有凹槽的金属圆环,沿其直径装有一根长2L的金属杆AC,可绕通过圆环中心的水平轴O转动.将一根质量不计的足够长细绳一端固定于槽内并将绳绕于圆环槽内,绳子的另一端悬挂了一个质量为m的物体.圆环的一半处在磁感应强度为B,方向垂直环面向里的匀强磁场中.现将物体由静止释放,若金属圆环和金属杆单位长度的电阻均为R.忽略所有摩擦和空气阻力.
如图所示,一个边缘带有凹槽的金属圆环,沿其直径装有一根长2L的金属杆AC,可绕通过圆环中心的水平轴O转动.将一根质量不计的足够长细绳一端固定于槽内并将绳绕于圆环槽内,绳子的另一端悬挂了一个质量为m的物体.圆环的一半处在磁感应强度为B,方向垂直环面向里的匀强磁场中.现将物体由静止释放,若金属圆环和金属杆单位长度的电阻均为R.忽略所有摩擦和空气阻力.(1)设某一时刻圆环转动的角速度为ω0,且OA边在磁场中,请求出此时金属杆OA产生电动势的大小;
(2)请求出物体在下落中可达到的最大速度;
(3)当物体下落达到最大速度后,金属杆OC段刚要进入磁场时,杆的A、O两端之间电压多大?
分析 (1)已知金属杆转动的角速度,根据:$E=\overline{v}BL$求出金属杆切割测磁感线产生的感应电动势;
(2)根据欧姆定律求出金属杆中的电流,根据安培力的公式求得金属杆受到的安培力,最后求出物体下落的最大速度;
(3)根据串联电路的分压特点即可求出CO两端的电压.
解答 解:(1)已知金属杆转动的角速度,OA产生的电动势:$E=BL•\frac{{ω}_{0}L}{2}=\frac{1}{2}B{L}^{2}{ω}_{0}$
(2)等效电路如图所示,两个半圆部分的电阻并联后与另一半半径上的电阻串联,
${R}_{外1}=\frac{πLR}{2}$
R外2=LR
r=LR
当达到最大速度时,重物的重力的功率等于电路中消耗的电功率:
$mgv=\frac{{E}^{2}}{{R}_{总}}=\frac{{E}^{2}}{{R}_{外1}+{R}_{外2}+r}$
其中:v=ω0L
联立以上公式,解得:$v=\frac{2mgR(4+π)}{{B}^{2}L}$
(3)当物体下落达到最大速度后,杆受到的安培力的力矩与物体的力矩相等,得:
$BIL•\frac{L}{2}=mg•L$
所以OA上的电流大小为:$I=\frac{2mg}{BL}$
当OC段在磁场中时,
${U}_{AO}=\frac{2mg}{BL}(\frac{πLR}{2}+LR)=\frac{2mgR}{B}(1+\frac{π}{2})$
答:(1)设某一时刻圆环转动的角速度为ω0,且OA边在磁场中,此时金属杆OA产生电动势的大小是$\frac{1}{2}B{L}^{2}{ω}_{0}$.
(2)物体在下落中可达到的最大速度$v=\frac{2mgR(4+π)}{{B}^{2}L}$.
(3)当物体下落达到最大速度后,金属杆OC段进入磁场时,杆A、O两端电压是$\frac{2mgR}{B}(1+\frac{π}{2})$.
点评 本题考查了求安培力的功率、产生的内能,求出感应电动势、安培力、应用能量守恒定律即可正确解题.

 如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )
如图所示的交变电压是矩形线框在匀强磁场内绕垂直于磁场的轴匀速转动过程中产生的,下列说法中正确的是( )| A. | 交变电压的有效值为$\sqrt{2}V$ | |
| B. | 0~4s内交变电压的平均值为$\frac{\sqrt{2}}{2}V$ | |
| C. | 1s末线框平面平行于磁场,通过线框的磁通量变化最快 | |
| D. | 2s时通过线框的磁通量为零 |
 如图所示,在光滑绝缘水平面上有一半径为R的圆,AB是一条直径,空间有匀强电场,场强大小为E,方向与水平面平行.在圆上A点有一发射器,以相同的动能平行于水平面沿不同方向发射带电量为+q的小球,小球会经过圆周上不同的点,在这些点中,经过C点的小球动能最大,由于发射时刻不同时,小球间无相互作用,且∠α=30°,下列说法正确的是( )
如图所示,在光滑绝缘水平面上有一半径为R的圆,AB是一条直径,空间有匀强电场,场强大小为E,方向与水平面平行.在圆上A点有一发射器,以相同的动能平行于水平面沿不同方向发射带电量为+q的小球,小球会经过圆周上不同的点,在这些点中,经过C点的小球动能最大,由于发射时刻不同时,小球间无相互作用,且∠α=30°,下列说法正确的是( )| A. | 电场的方向垂直AB向上 | |
| B. | 电场的方向垂直AB向下 | |
| C. | 小球在A点垂直电场方向发射,若恰能落到C点,则初动能为$\frac{qER}{8}$ | |
| D. | 小球在A点垂直电场方向发射,若恰能落到C点,则初动能为$\frac{qER}{4}$ |
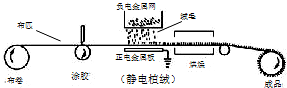 如图,静电植绒时,真空中带负电的绒毛一旦与布匹上的粘合剂接触就粘贴在布匹上,则带负电绒毛落向布匹的过程中( )
如图,静电植绒时,真空中带负电的绒毛一旦与布匹上的粘合剂接触就粘贴在布匹上,则带负电绒毛落向布匹的过程中( )| A. | 做匀速运动 | B. | 做加速运动 | C. | 电势能逐渐增大 | D. | 电势能逐渐减小 |
 如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )
如图所示,一个圆形框架以竖直的直径为转轴匀速转动.在框架上套着两个质量相等的小球A、B,小球A、B到竖直转轴的距离相等,它们与圆形框架保持相对静止.下列说法正确的是( )| A. | 小球A的合力小于小球B的合力 | |
| B. | 小球A与框架间可能没有摩擦力 | |
| C. | 小球B与框架间可能没有摩擦力 | |
| D. | 圆形框架以更大的角速度转动,小球B受到的摩擦力一定增大 |
 如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做完整的圆周运动,则下列说法中正确的是( )
如图所示,用长为L的细绳拴着质量为m的小球在竖直平面内做完整的圆周运动,则下列说法中正确的是( )| A. | 小球运动到最高点时所受的向心力不一定等于重力 | |
| B. | 小球在最高点时绳子的拉力不可能为零 | |
| C. | 小球运动到最高点的速率一定大于$\sqrt{gL}$ | |
| D. | 小球经过最低点时绳子的拉力一定大于小球重力 |

 的内电阻并且要想得到较高的精确度,那么以上给出的器材中,电阻Rl应选用E,电阻R2应选用C,电源应选用G.(填写所选仪器前的字母即可)
的内电阻并且要想得到较高的精确度,那么以上给出的器材中,电阻Rl应选用E,电阻R2应选用C,电源应选用G.(填写所选仪器前的字母即可) 的内阻Rg的测量值为200Ω,该测量值比实际值略小(选填“大”、“小”).
的内阻Rg的测量值为200Ω,该测量值比实际值略小(选填“大”、“小”). 改装成量程为2V的电压表,则改装的方法是电流表应串联一个阻值为9800Ω的电阻.
改装成量程为2V的电压表,则改装的方法是电流表应串联一个阻值为9800Ω的电阻. 与电阻箱改装成一电压表.现要对此电压表进行校准,所用的电路原理如图2所示,图3中给出了实验器材的实物图,请按原理图的要求连成实验电路.
与电阻箱改装成一电压表.现要对此电压表进行校准,所用的电路原理如图2所示,图3中给出了实验器材的实物图,请按原理图的要求连成实验电路.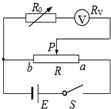 某同学采用“半偏法”测量一个量程为3V的电压表的内阻.
某同学采用“半偏法”测量一个量程为3V的电压表的内阻.