题目内容
16. 如图所示,在光滑绝缘水平面上有一半径为R的圆,AB是一条直径,空间有匀强电场,场强大小为E,方向与水平面平行.在圆上A点有一发射器,以相同的动能平行于水平面沿不同方向发射带电量为+q的小球,小球会经过圆周上不同的点,在这些点中,经过C点的小球动能最大,由于发射时刻不同时,小球间无相互作用,且∠α=30°,下列说法正确的是( )
如图所示,在光滑绝缘水平面上有一半径为R的圆,AB是一条直径,空间有匀强电场,场强大小为E,方向与水平面平行.在圆上A点有一发射器,以相同的动能平行于水平面沿不同方向发射带电量为+q的小球,小球会经过圆周上不同的点,在这些点中,经过C点的小球动能最大,由于发射时刻不同时,小球间无相互作用,且∠α=30°,下列说法正确的是( )| A. | 电场的方向垂直AB向上 | |
| B. | 电场的方向垂直AB向下 | |
| C. | 小球在A点垂直电场方向发射,若恰能落到C点,则初动能为$\frac{qER}{8}$ | |
| D. | 小球在A点垂直电场方向发射,若恰能落到C点,则初动能为$\frac{qER}{4}$ |
分析 小球在匀强电场中,从A点运动到C点,根据动能定理qUAC=Ek,因为到达C点时的小球的动能最大,所以UAC最大,即在圆周上找不到与C电势相等的点.所以与C点电势相等的点在过C点的切线上.再根据电场线与等势线垂直,可以画出电场线,即可确定电场的方向.
小球做类平抛运动,根据平抛运动的知识分析小球的运动情况,分别相互垂直的两个上列式求解初动能
解答  解:A、B:小球在匀强电场中,从a点运动到c点,根据动能定理qUAC=Ek得
解:A、B:小球在匀强电场中,从a点运动到c点,根据动能定理qUAC=Ek得
因为到达C点时的小球的动能最大,所以UAC最大,则在圆周上找不到与C电势相等的点.且由A到C电场力对小球做正功.
过C点作切线,则CF为等势线.
过A点作CF的垂线,则该线为电场线,场强方向如图示.
因为∠CAB=30°,则连接CO,∠ACO=30°,所以电场方向与AC间的夹角θ为30°;故AB错误.
C、D:小球只受电场力,做类平抛运动.
x=Rcos30°=v0t,
y=R+Rsin30°=$\frac{qE{t}^{2}}{2m}$,
由以上两式得:Ek=$\frac{1}{2}$mv02=$\frac{1}{8}$qER;故C正确,D错误
故选:C
点评 本题关键考查对电场力做功公式W=qEd的理解和应用,d是沿电场方向两点间的距离.此题还要求熟练掌握功能关系和类平抛运动的研究方法

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
6.伽利略开创了实验研究和逻辑推理相结合探索物理规律的科学方法,利用这种方法伽利略发现的规律有( )
| A. | 力不是维持物体运动的原因 | |
| B. | 忽略空气阻力,重物与轻物下落得同样快 | |
| C. | 物体之间普遍存在相互吸引力 | |
| D. | 物体间的相互作用力总是大小相等,方向相反 |
7.物体做匀速直线运动,下列物理量保持恒定的是( )
| A. | 速度 | B. | 位移 | C. | 路程 | D. | 加速度 |
4.一定质量的理想气体,压强保持不变,当温度为27℃时,体积为V,当温度升高到81℃时,体积变为( )
| A. | 3V | B. | 2V | C. | 1.18V | D. | $\frac{V}{3}$ |
11.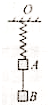 如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )
如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )
 如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )
如图所示,轻质弹簧一端悬于O点,另一端系物体A,物体A下用轻绳挂着物体B,系统处于静止状态.现剪断轻绳,物体A上升至最高点时弹簧恰好回复原长,则物体A,B的质量关系为( )| A. | mA=mB | B. | mA>mB | C. | mA<mB | D. | 无法确定 |
1.一个质量为m的带电小球,在竖直方向的匀强电场中水平抛出,不计空气阻力,测得小球的加速度大小为$\frac{g}{3}$,方向向下,其中g为重力加速度.则在小球下落h高度的过程中,下列说法正确的是( )
| A. | 小球的动能增加$\frac{2}{3}$mgh | B. | 小球的电势能减小$\frac{2}{3}$mgh | ||
| C. | 小球的重力势能减少$\frac{1}{3}$mgh | D. | 小球的机械能减少$\frac{2}{3}$mgh |
6. 一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )
一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )
 一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )
一匀强磁场,磁场方向垂直纸面,规定向里的方向为正,在磁场中有一细金属圆环,线圈位于纸面内,如图甲所示.现令磁感应强度值B随时间t变化,先按图乙所示的Oa图线变化,后来又按bc和cd变化,令E1、E2、E3分别表示这三段变化过程中感应电动势的大小,I1、I2、I3分别表示对应的感应电流( )| A. | E1>E2,I1沿逆时针方向,I2沿顺时针方向 | |
| B. | E1<E2,I1沿逆时针方向,I2沿顺时针方向 | |
| C. | E1<E2,I2沿顺时针方向,I3沿逆时针方向 | |
| D. | E2=E3,I2沿顺时针方向,I3沿顺时针方向 |
 如图所示,一个边缘带有凹槽的金属圆环,沿其直径装有一根长2L的金属杆AC,可绕通过圆环中心的水平轴O转动.将一根质量不计的足够长细绳一端固定于槽内并将绳绕于圆环槽内,绳子的另一端悬挂了一个质量为m的物体.圆环的一半处在磁感应强度为B,方向垂直环面向里的匀强磁场中.现将物体由静止释放,若金属圆环和金属杆单位长度的电阻均为R.忽略所有摩擦和空气阻力.
如图所示,一个边缘带有凹槽的金属圆环,沿其直径装有一根长2L的金属杆AC,可绕通过圆环中心的水平轴O转动.将一根质量不计的足够长细绳一端固定于槽内并将绳绕于圆环槽内,绳子的另一端悬挂了一个质量为m的物体.圆环的一半处在磁感应强度为B,方向垂直环面向里的匀强磁场中.现将物体由静止释放,若金属圆环和金属杆单位长度的电阻均为R.忽略所有摩擦和空气阻力. 于B点,整个轨道处在竖直向下的匀强电场中,一不带电的绝缘小球甲,以速度v0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞.已知甲、乙两球的质量均为m,重力加速度为g,且乙球所受电场力与乙球重力mg相等.水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移.
于B点,整个轨道处在竖直向下的匀强电场中,一不带电的绝缘小球甲,以速度v0沿水平轨道向右运动,与静止在B点带正电的小球乙发生弹性碰撞.已知甲、乙两球的质量均为m,重力加速度为g,且乙球所受电场力与乙球重力mg相等.水平轨道足够长,甲、乙两球可视为质点,整个运动过程无电荷转移.