题目内容
甲、乙两船在同一条河流中同时开始渡河，河宽为H，河水流速为v0，船在静水中的速度均为v，出发时两船相距
，甲、乙两船船头均与河岸成60°，如图所示。已知乙船恰好能垂直到达对岸A点，则下列判断正确的是
| A．甲、乙两船到达对岸的时间不同 | B．v=2v0 |
| C．两船可能在未到达对岸前相遇 | D．甲船不在A点靠岸 |
B
解析试题分析：因为两船在静水中的速度相同，船头指向也相同，所以船过河的速度也相同，均为vsin60°,所以甲、乙两船到达对岸的时间相同，且均为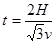
，A选项错误；因为乙船恰好能垂直到达对岸，则vcos60°=v0,即v=2v0，选项B正确；两船相遇所用时间为
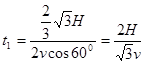，所以两船正好在到达对岸时相遇，C选项错；到达河岸时甲船沿河岸方向的位移为x=(vcos60°+v0)t=,所以甲船正好在A点靠岸，D选项错误。
考点：速度的合成和分解。
练习册系列答案
津桥教育计算小状元系列答案
相关题目
如图所示，MN是流速稳定的河流，河宽一定，小船在静水中的速度为v.现小船自A点渡河，第一次船头沿AB方向，到达对岸的D处；第二次船头沿AC方向，到达对岸E处，若AB与AC跟河岸垂线AD的夹角相等，两次航行的时间分别为tB、tC，则（ ）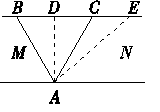
| A．tB>tC | B．tB<tC |
| C．tB＝tC | D．无法比较tB与tC的大小 |
一条小船在静水中的速度为3 m/s，它要渡过一条宽为30 m的长直河道，河水流速为4 m/s，则（ ）
| A．这条船不可能渡过这条河 |
| B．这条船过河时间不可能小于10 s |
| C．这条船能够过河的最小位移为30m |
| D．这条船可以渡过这条河，而且过河时的合速度可以为8m/s |
如图所示，小船以大小为
、方向与上游河岸成θ的速度（在静水中的速度）从A处过河，经过t时间，正好到达正对岸的B处。现要使小船在更短的时间内过河并且也正好到达正对岸B处，在水流速度不变的情况下，可采取下列方法中的哪一种( )
| A．只要增大大小，不必改变θ角 |
| B．只要增大θ角，不必改变大小 |
| C．在增大的同时，也必须适当减小θ角 |
| D．在增大的同时，也必须适当增大θ角 |
一颗小行星环绕太阳作匀速圆周运动，半径是地球环绕半径的4倍，则它的环绕周期是（ ）
| A．2年 | B．4年 | C．8年 | D．16年 |
关于三个宇宙速度，下列说法正确的是 （ ）
| A．第一宇宙速度是卫星环绕行星的最小运行速度 |
| B．地球的第二宇宙速度大小为16.7km/s |
| C．当人造地球卫星的发射速度达到第二宇宙速度时，卫星就逃出太阳系了 |
| D．地球同步卫星在轨道上运行的速度一定小于第一宇宙速度 |