题目内容
如图所示,小船以大小为 、方向与上游河岸成θ的速度(在静水中的速度)从A处过河,经过t时间,正好到达正对岸的B处。现要使小船在更短的时间内过河并且也正好到达正对岸B处,在水流速度不变的情况下,可采取下列方法中的哪一种( )
、方向与上游河岸成θ的速度(在静水中的速度)从A处过河,经过t时间,正好到达正对岸的B处。现要使小船在更短的时间内过河并且也正好到达正对岸B处,在水流速度不变的情况下,可采取下列方法中的哪一种( )
A.只要增大 大小,不必改变θ角 大小,不必改变θ角 |
B.只要增大θ角,不必改变 大小 大小 |
C.在增大 的同时,也必须适当减小θ角 的同时,也必须适当减小θ角 |
D.在增大 的同时,也必须适当增大θ角 的同时,也必须适当增大θ角 |
D
解析试题分析:
法一:小船过河的时间取决于垂直河岸方向的速度,即为v1sinθ,要使小船到达B点,且时间变短,则v1sinθ应增大,同时小船在沿河岸方向的速度仍应为零,即v1cosθ的值不变,因此需要增大v1,同时增大θ角,故选项D正确。
法二:可以采用作图法:如解图所示,故选项D正确。
考点:本题主要考查运动的合成与分解问题,属于中档题。

练习册系列答案
相关题目
一小船在静水中的速度为5 m/s,它在一条河宽为200 m,水流速度为3 m/s的河流中过河,则( )
| A.小船不可能垂直河岸抵达正对岸 |
| B.小船过河的时间不可能少于50 s |
| C.小船以最短航程过河时,过河的时间为40 s |
| D.小船以最短时间过河时,它沿水流方向的位移大小为120 m |
一条河宽100m,船在静水中的速度为4m/s,水流速度是5m/s,则 ( )
| A.该船能垂直河岸横渡到对岸 |
| B.当船头垂直河岸横渡时,过河所用的时间最短 |
| C.当船头垂直河岸横渡时,船的位移最小,是100m |
| D.该船渡到对岸时,船对岸的位移可能小于100m |
甲、乙两船在同一条河流中同时开始渡河,河宽为H,河水流速为v0,船在静水中的速度均为v,出发时两船相距 ,甲、乙两船船头均与河岸成60°,如图所示。已知乙船恰好能垂直到达对岸A点,则下列判断正确的是
,甲、乙两船船头均与河岸成60°,如图所示。已知乙船恰好能垂直到达对岸A点,则下列判断正确的是
| A.甲、乙两船到达对岸的时间不同 | B.v=2v0 |
| C.两船可能在未到达对岸前相遇 | D.甲船不在A点靠岸 |
举世瞩目的“神舟”六号航天飞船的成功发射和顺利返回,显示了我国航天事业取得的巨大成就,已知地球的质量为M,引力常量为G,设飞船绕地球做匀速圆周运动的轨道半径为r,则飞船在圆轨道上运行的速率为( )
A. | B. | C.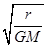 | D. |
我国发射的“嫦娥一号”卫星经过多次加速、变轨后,最终成功进入环月工作轨道。如图所示,卫星既可以在离月球比较近的圆轨道a上运动,也可以在离月球比较远的圆轨道b上运动。下列说法正确的是( )
| A.卫星在a上运行的线速度小于在b上运行的线速度 |
| B.卫星在a上运行的周期大于在b上运行的周期 |
| C.卫星在a上运行的角速度小于在b上运行的角速度 |
| D.卫星在a上运行时受到的万有引力大于在b上运行时的万有引力 |

 F
F F
F