题目内容
10.甲乙两物体在同一条直线上同时同地沿同一方向运动,甲初速度为6m/s,由于摩擦做匀减速直线运动,加速度大小为2m/s2;乙做初速度为零,加速度为1m/s2的匀加速直线运动.求:(1)甲物体能运动多远?
(2)乙此后经多长时间追上甲?
(3)乙追上甲之前两物体最大距离是多少?
分析 (1)根据匀变速直线运动的速度位移公式求出甲物体能够运动的距离.
(2)根据甲乙的位移关系,结合运动学公式求出追及的时间.
(3)当甲乙的速度相等时,相距最远,结合位移公式求出相距的最大距离.
解答 解:(1)根据匀变速直线运动的速度位移公式得,甲物体能够运动的距离${x}_{1}=\frac{0-{{v}_{0}}^{2}}{2a}=\frac{-36}{-4}m=9m$.
(2)甲物体速度减为零的时间${t}_{1}=\frac{0-{v}_{0}}{a}=\frac{-6}{-2}s=3s$,
此时乙的位移${x}_{2}=\frac{1}{2}a′{{t}_{1}}^{2}=\frac{1}{2}×1×9m=4.5m$,
可知甲物体停止时,乙物体还为追上甲,
根据${x}_{1}=\frac{1}{2}a′{t}^{2}$得,追及的时间$t=\sqrt{\frac{2{x}_{1}}{a′}}=\sqrt{\frac{2×9}{1}}s=3\sqrt{2}s$.
(3)当甲乙速度相等时,相距最远,设速度相等经历的时间为t′,
有v0+at′=a′t′,解得$t′=\frac{{v}_{0}}{a′-a}=\frac{6}{1+2}s=2s$,
则相距的最远距离$△x={v}_{0}t′+\frac{1}{2}at{′}^{2}-\frac{1}{2}a′t{′}^{2}$=$6×2-\frac{1}{2}×2×4-\frac{1}{2}×1×4m=6m$.
答:(1)甲物体能运动9m.
(2)乙此后经$3\sqrt{2}s$时间追上甲.
(3)乙追上甲之前两物体最大距离是6m.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式灵活求解,知道速度相等时甲乙相距最远.

| A. | 上述过程的加速度大小为0.2m/s2 | B. | 刹车过程持续的时间为2s | ||
| C. | t=0时刻的速度为5m/s | D. | 刹车过程的位移为5m |
 如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落到斜面时的速度与斜面的夹角α,若把初速度变为2v0,且小球仍落在斜面上,则以下说法错误的是( )
如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落到斜面时的速度与斜面的夹角α,若把初速度变为2v0,且小球仍落在斜面上,则以下说法错误的是( )| A. | 小球在空中运动的时间变为原来的2倍 | |
| B. | 落点Q与P的距离变为原来的2倍 | |
| C. | 落到斜面时的速度与斜面夹角α不变 | |
| D. | 落到斜面时的动能变为原来的4倍 |
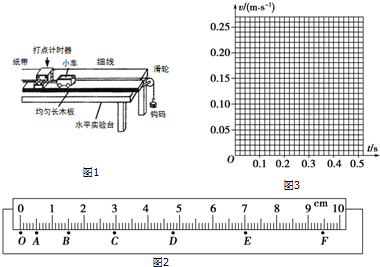
(1)将下列步骤的代号按合理顺序填写在横线上:BECADF
A.将小车移至靠近打点计时器处,先接通电源,后放开纸带
B.将打点计时器固定在平板上,并接好电路
C.把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着重量适当的钩码
D.断开电源,取下纸带
E.将纸带固定在小车尾部,并穿过打点计时器的限位孔
F.换上新的纸带,再重复做三次.
(2)某同学得到一条用打点计时器打下的纸带,并在其上取了O、A、B、C、D、E、F共7个计数点(图中每相邻两个记数点间还有四个打点计时器打下的点未画出),如图2所示.打点计时器接的是50Hz的低压交流电源.他将一把毫米刻度尺放在纸带上,其零刻度和记数点O对齐,从刻度尺上直接读取数据记录在表中.
| 线段 | OA | OB | OC | OD | OE | OF |
| 数据/cm | 0.54 | 1.53 | 2.92 | 4.76 | 7.00 | 9.40 |
| 各点速度 | vA | vB | vC | vD | vE |
| 数据/(×10-2m/s) | 7.70 | 12.0 | 16.2 | 20.4 |
②试根据表格中数据和你求得的E点速度在图3所给的坐标中,用铅笔和直尺作出v-t图象,从图象中求得物体的加速度a=0.42m/s2(加速度取两位有效数字)
| A. | 速度变化很大,加速度很小 | |
| B. | 速度变化方向为正,加速度方向为正 | |
| C. | 速度变化越来越快,加速度越来越小 | |
| D. | 速度越来越大,加速度越来越小 |
| A. | 20 m/s2 | B. | 40 m/s2 | C. | 60 m/s2 | D. | 100 m/s2 |
 如图所示是某质点运动的v-t图象,请回答:
如图所示是某质点运动的v-t图象,请回答: