题目内容
1. 如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落到斜面时的速度与斜面的夹角α,若把初速度变为2v0,且小球仍落在斜面上,则以下说法错误的是( )
如图所示,从倾角为θ的足够长的斜面顶端P以速度v0抛出一个小球,落在斜面上某处Q点,小球落到斜面时的速度与斜面的夹角α,若把初速度变为2v0,且小球仍落在斜面上,则以下说法错误的是( )| A. | 小球在空中运动的时间变为原来的2倍 | |
| B. | 落点Q与P的距离变为原来的2倍 | |
| C. | 落到斜面时的速度与斜面夹角α不变 | |
| D. | 落到斜面时的动能变为原来的4倍 |
分析 小球在空中做平抛运动,小球落在斜面上时,根据竖直位移与水平位移之比等于tanθ求出小球在空中的运动时间,从而得出P、Q间距离的变化.结合速度方向与水平方向夹角正切值和位移与水平方向夹角正切值的关系,判断夹角与初速度的关系.由速度的合成法分析落到斜面时的速度如何弯,从而判断动能如何变化.
解答 解:A、根据tanθ=$\frac{y}{x}$=$\frac{\frac{1}{2}g{t}^{2}}{{v}_{0}t}$=$\frac{gt}{2{v}_{0}}$得,t=$\frac{2{v}_{0}tanθ}{g}$,则知初速度变为原来的2倍,则小球在空中的运动时间变为原来的2倍.故A正确.
B、根据x=v0t=$\frac{2{v}_{0}^{2}tanθ}{g}$知,初速度变为原来的2倍,则水平位移变为原来的4倍,则P、Q间距变为原来的4倍.故B错误.
C、小球落到斜面上时,速度与水平方向夹角的正切值 tanβ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{gt}{{v}_{0}}$=2tanθ,则知速度方向与水平方向夹角不变,所以两个角度之差,即α不变,与初速度无关.故C正确.
D、落到斜面时的速度大小为 v=$\sqrt{{v}_{0}^{2}+{v}_{y}^{2}}$=$\sqrt{{v}_{0}^{2}+(gt)^{2}}$=v0$\sqrt{1+4ta{n}^{2}θ}$,则知落到斜面时的速度大小变为原来的2倍,落到斜面时的动能变为原来的4倍,故D正确.
本题选错误的,故选:B
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,知道某时刻速度方向与水平方向夹角正切值是位移与水平方向夹角正切值的2倍这一结论.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
11.国外研发出一种吸盘式手套,把吸盘紧压在墙上,开动抽气机抽出吸盘中的空气,使人能在竖直墙面上攀爬,当人静止在墙上时,让抽气机抽出更多空气,这时( )
| A. | 吸盘受到的摩擦力变大 | B. | 吸盘受到的摩擦力变小 | ||
| C. | 吸盘对墙壁的压力变大 | D. | 吸盘对墙壁的压力变小 |
12.如图所示,物体静止在固定的斜面上,则对物体的受力分析,下列正确的是( )


| A. | 重力、支持力、压力 | B. | 重力、支持力、摩擦力 | ||
| C. | 重力、下滑力、支持力、摩擦力 | D. | 重力、下滑力、支持力、压力、摩擦力 |
16.甲、乙两车在平直公路上同向行驶,其v-t图象如图所示.已知两车在t=1s时并排行驶,则( ) 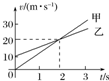

| A. | 在t=2 s时,乙车在甲车后 | |
| B. | 在t=0时,乙车在甲车前10m | |
| C. | 两车另一次并排行驶的时刻是t=3s | |
| D. | 甲、乙车两次并排行驶的位置之间沿公路方向的距离为40 m |
6.在物理学的发展过程中,科学家们创造出了许多物理学研究方法,以下关于所用物理学研究方法的叙述正确的是( )
| A. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了理想模型法 | |
| B. | 通过做大量实验后,胡克认为弹力一定与弹簧的形变量成正比 | |
| C. | 伽利略认为自由落体运动就是物体在倾角为90°的斜面上的运动.再根据铜球在斜面上的运动规律得出自由落体的运动规律,这是采用了实验和逻辑推理相结合的方法 | |
| D. | 在不需要考虑带电物体本身的大小和形状时,用点电荷来代替物体的方法叫微元法 |
13. 如图所示,小车放在水平地面上甲乙二人用力向相反方向拉小车,不计小车与地面之间的摩擦力,下面说法正确的是( )
如图所示,小车放在水平地面上甲乙二人用力向相反方向拉小车,不计小车与地面之间的摩擦力,下面说法正确的是( )
 如图所示,小车放在水平地面上甲乙二人用力向相反方向拉小车,不计小车与地面之间的摩擦力,下面说法正确的是( )
如图所示,小车放在水平地面上甲乙二人用力向相反方向拉小车,不计小车与地面之间的摩擦力,下面说法正确的是( )| A. | 甲拉小车的力和乙拉小车的力是一对作用力和反作用力 | |
| B. | 小车静止时甲拉小车的力和乙拉小车的力是一对平衡力 | |
| C. | 若小车加速向右运动表明小车拉甲的力大于甲拉小车的力 | |
| D. | 若小车加速向右运动表明乙拉小车的力大于小车拉乙的力 |
11.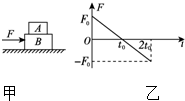 如图甲所示,A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一水平变力的作用,该力与时间的关系如图乙所示,A、B始终相对静止,则下列说法正确的是( )
如图甲所示,A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一水平变力的作用,该力与时间的关系如图乙所示,A、B始终相对静止,则下列说法正确的是( )
 如图甲所示,A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一水平变力的作用,该力与时间的关系如图乙所示,A、B始终相对静止,则下列说法正确的是( )
如图甲所示,A、B两物体叠放在一起,放在光滑的水平面上,从静止开始受到一水平变力的作用,该力与时间的关系如图乙所示,A、B始终相对静止,则下列说法正确的是( )| A. | 在t0时刻,A、B之间的摩擦力最大 | |
| B. | 在t0时刻,A、B的速度最大 | |
| C. | 2t0时刻,A、B回到出发点 | |
| D. | 在0~2 t0时间内,摩擦力对A做功为零 |
