题目内容
如图所示，小车上有固定支架，支架上用细线拴一个小球，线长为l（小球可看作质点），小车与小球一起以速度v0沿水平方向向左匀速运动。当小车突然碰到矮墙后车立即停止运动，此后小球升高的最大高度可能是（线未被拉断）（ ）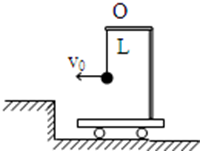
A．大于 | B．小于 |
C．等于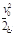 | D．等于2l |
BCD
解析试题分析: 如果小球的速度不能使小球做圆周运动，由机械能守恒可得，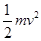
=mgh，所以最大高度可能是
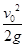，所以A错，C对；如果有空气的阻力的话，机械能不守恒，最大高度就要小于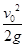，所以B正确；如果小球的速度能使小球做圆周运动，那么最大的高度就是圆周运动的直径2L，所以D正确
考点：机械能守恒定律，动能定理，牛顿第二定律，向心力
阳光试卷单元测试卷系列答案如图所示，长木板放置在水平面上，一小物块置于长木板的中央，长木板和物块的质量均为m，物块与木板间的动摩擦因数为μ，木板与水平面间动摩擦因数
，已知最大静摩擦力与滑动摩擦力大小相等，重力加速度为g．现对物块施加一水平向右的拉力F，则木板加速度大小a可能是 （ ）
| A．a＝μg | B．a＝ |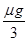
C．a＝ | D．a＝ － |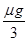
迪拜塔超过160层，且拥有56部电梯，速度最高达每秒17.4米，那将是世界上速度最快且运行距离最长的电梯,则一部电梯从第160层下降到底层的过程中（阻力不计）（ ）
| A．缆绳对电梯拉力的大小一定小于重力 |
| B．缆绳对电梯拉力做功的大小一定等于重力所做的功 |
| C．电梯下降过程速度取最大值时，加速度一定最小 |
| D．电梯发动机做恒定功率运行 |
如图所示，三角体由两种材料拼接而成，BC界面平行底面DE，且B点为AD的中点，两侧面与水平面夹角分别为37
。和53。已知一物块从A静止下滑，加速至B减速至D，且到D点时恰好静止。若该物块从A点静止释放沿另一侧面下滑，则有 （ ）
| A．通过C点的速率大于通过B点的速率 |
| B．AC段加速，CE段减速 |
| C．到达E点时速度大于零 |
| D．一直加速运动到E，但AC段的加速度比CE段小 |
如图所示，质量为m的物体用细绳拴住放在水平粗糙传送带上，物体距传送带左端距离为L，稳定时绳与水平方向的夹角为θ.当传送带分别以v1、v2的速度作逆时针转动时（v1<v2），绳中的拉力分别为Fl、F2；若剪断细绳时，物体一直匀加速运动到达左端时，所用的时间分别为tl、t2，则下列说法正确的是
| A．Fl<F2 | B．F1=F2 |
| C．tl=t2 | D．tl<t2 |
狄拉克曾经预言，自然界应该存在只有一个磁极的磁单极子，其周围磁感线呈均匀辐射状分布，距离它r处的磁感应强度大小为B=
(k为常数)。磁单极S的磁场分布如图甲所示，它与如图乙所示负点电荷Q的电场分布相似。假设磁单极子S和负点电荷Q均固定，有一带电小球分别在S和Q附近做匀速圆周运动，则关于小球做匀速圆周运动的判断正确的是
| A．若小球带正电，其运动轨迹平面可在S正上方，如图甲所示 |
| B．若小球带正电，其运动轨迹平面可在Q正下方，如图乙所示 |
| C．若小球带负电，其运动轨迹平面可在S正上方，如图甲所示 |
| D．若小球带负电，其运动轨迹平面可在Q正下方，如图乙所示 |
如图所示，小车上固定一水平横杆，横杆左端的固定斜杆与竖直方向成α角，斜杆下端连接一质量为m的小球；横杆右端用一根细线悬挂相同的小球。当小车沿水平面做直线运动时，细线与竖直方向间的夹角β(β≠α)保持不变。设斜杆、细线对小球的作用力分别为F1、F2，下列说法正确的是( )
| A．F1、F2大小相等 | B．F1、F2方向相同 |
| C．小车加速度大小为gtanα | D．小车加速度大小为gtanβ |
