题目内容
15.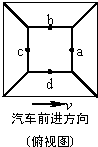 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )| A. | Ta=Tb=Td=Tc,Ea>Eb=Ed>Ec | B. | Ta=Tb=Td=Tc,Ea=Eb=Ed=Ec | ||
| C. | Ta<Tb=Td<Tc,Ea>Eb=Ed>Ec | D. | Ta<Tb=Td<Tc,Ea=Eb=Ed=Ec |
分析 分别以棱台和地面为参考系,根据相对运动规律确定小球的运动状态,根据功的定义可确定做功情况; 从而确定落地时的动能.
解答 解:以棱台为参考系,以释放点为原点建立坐标系
水平方向的加速度:ax=gsinθcosθ
竖直加速度:ay=gsinθsinθ
对于前放释放的小球
水平位移:x=$\frac{1}{2}$gsinθcosθt2
竖直位移:y=$\frac{1}{2}$gsinθsinθt2
以地面为参考系,以释放点为原点建立坐标系
水平位移:X=vt+$\frac{1}{2}$gsinθcosθt2
竖直位移:Y=$\frac{1}{2}$gsinθsinθt2
对于后放释放的小球,以棱台为参考系,以释放点为原点建立坐标系
水平位移:x=-$\frac{1}{2}$gsinθcosθt2
竖直位移:y=$\frac{1}{2}$gsinθsinθt2
在地面为参考系,在前方小球同一坐标系下
水平方向上的位移:X=vt-$\frac{1}{2}$gsinθcosθt2-d
竖直方向上的位移:Y=$\frac{1}{2}$gsinθsinθt2
竖直方向遵循同一方程,故下落时间一定相同;
根据功的定义可知,在水平方向,因a受支持力做正功,而c受支持力做负功;bd受到的支持力不做功; 故前者水平速度大,故前者落地时的机械能大;Ea>Eb=Ed>Ec
故A正确,BCD错误;
故选:A
点评 本题要注意正确选择参考平面,建立坐标系,由运动学规律分析物体的运动过程,再由能量关系确定落地时的机械能;由于情景较为复杂,故对学生分析能力要求较高;要求能正确根据题意选择参考系进行分析才能准确判断小球的运动情况.

练习册系列答案
相关题目
5.下列关于功的说法中正确的是( )
| A. | 由于功有正、负,所以功是矢量 | |
| B. | 计算式W=Flcosα中,F是力的大小,l是位移的大小,α是力和位移间的夹角 | |
| C. | 合力对物体做的功,等于各分力做的功的矢量和 | |
| D. | 合力对物体做的功,等于各分力做的功的代数和 |
3. 如图示为电场中的一组等势面,若A,B,C,D相邻两点间距离均为2cm,A和P两点间的距离为1.5cm,则该电场的电场强度E和P点的电势φP分别为( )
如图示为电场中的一组等势面,若A,B,C,D相邻两点间距离均为2cm,A和P两点间的距离为1.5cm,则该电场的电场强度E和P点的电势φP分别为( )
 如图示为电场中的一组等势面,若A,B,C,D相邻两点间距离均为2cm,A和P两点间的距离为1.5cm,则该电场的电场强度E和P点的电势φP分别为( )
如图示为电场中的一组等势面,若A,B,C,D相邻两点间距离均为2cm,A和P两点间的距离为1.5cm,则该电场的电场强度E和P点的电势φP分别为( )| A. | 500 V/m,-2.5V | B. | $\frac{1000\sqrt{3}}{3}$V/m,-2.5V | C. | 500V/m,2.5V | D. | $\frac{1000\sqrt{3}}{3}$V/m,2.5V |
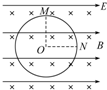 如图所示,半径为R的光滑绝缘环竖直置于彼此正交的水平匀强电场和垂直纸面向里的匀强磁场中,磁感应强度为B,今有一质量为m、带电荷量为+q的空心小球穿在环上,已知小球所受电场力和重力大小相等,则当小球由静止开始从环顶M下滑到与圆心等高的N点时,小球给环的压力大小为多少?
如图所示,半径为R的光滑绝缘环竖直置于彼此正交的水平匀强电场和垂直纸面向里的匀强磁场中,磁感应强度为B,今有一质量为m、带电荷量为+q的空心小球穿在环上,已知小球所受电场力和重力大小相等,则当小球由静止开始从环顶M下滑到与圆心等高的N点时,小球给环的压力大小为多少?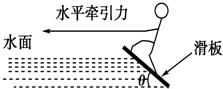 滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如上图所示),滑板做匀速直线运动,相应的k=45kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin 37°=$\frac{3}{5}$,忽略空气阻力):
滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力FN垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角θ=37°时(如上图所示),滑板做匀速直线运动,相应的k=45kg/m,人和滑板的总质量为108kg,试求(重力加速度g取10m/s2,sin 37°=$\frac{3}{5}$,忽略空气阻力): 如图所示,在光滑的水平面上,质量为4m、长为L的木板右端紧靠竖直墙壁,与墙壁不粘连;质量为m的小滑块(可视为质点)以水平速度v0滑到木板左端,滑到木板右端时速度恰好为零;现小滑块以水平速度v滑上木板左端,滑到木板右端时与竖直墙壁发生弹性碰撞,以原速率弹回,刚好能够滑到木板左端而不从木板上落下,求$\frac{v}{{v}_{0}}$的值.
如图所示,在光滑的水平面上,质量为4m、长为L的木板右端紧靠竖直墙壁,与墙壁不粘连;质量为m的小滑块(可视为质点)以水平速度v0滑到木板左端,滑到木板右端时速度恰好为零;现小滑块以水平速度v滑上木板左端,滑到木板右端时与竖直墙壁发生弹性碰撞,以原速率弹回,刚好能够滑到木板左端而不从木板上落下,求$\frac{v}{{v}_{0}}$的值. 猎豹是目前世界上在陆地奔跑速度最快的动物,时速可达110多公里,但不能维持长时间高速奔跑,否则会因身体过热而危及生命.猎豹在一次追击猎物时(如图),经4s速度由静止达到最大,然后匀速运动保持了4s仍没追上猎物,为保护自己它放弃了这次行动,以3m/s2的加速度减速,经10s停下,设此次追捕猎豹始终沿直线运动.求:
猎豹是目前世界上在陆地奔跑速度最快的动物,时速可达110多公里,但不能维持长时间高速奔跑,否则会因身体过热而危及生命.猎豹在一次追击猎物时(如图),经4s速度由静止达到最大,然后匀速运动保持了4s仍没追上猎物,为保护自己它放弃了这次行动,以3m/s2的加速度减速,经10s停下,设此次追捕猎豹始终沿直线运动.求: 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度vA=4m/s.g取10m/s2,求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度vA=4m/s.g取10m/s2,求: