题目内容
5. 如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度vA=4m/s.g取10m/s2,求:
如图,一个质量为0.6kg的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失).已知圆弧的半径R=0.3m,θ=60°,小球到达A点时的速度vA=4m/s.g取10m/s2,求:(1)小球做平抛运动的初速度v0;
(2)小球到达圆弧最高点C时对轨道的压力.
(3)若圆弧轨道粗糙,小球恰好能够经过最高点C,求此过程小球克服摩擦力所做的功.
分析 (1)恰好从光滑圆弧ABC的A点的切线方向进入圆弧,说明到到A点的速度vA方向与水平方向的夹角为θ,这样可以求出初速度v0;
(2)由动能定理求出小球到达C点时的速度,然后应用牛顿第二定律求出轨道对球的支持力,再求出压力;
(3)应用牛顿第二定律求出小球到达C点时的速度,然后应用动能定理求出克服摩擦力做的功.
解答 解:(1)小球恰好从光滑圆弧ABC的A点的切线方向进入圆弧,
小球到A点的速度与水平方向的夹角为θ,
小球的初速度:v0=vx=vAcosθ=4×0.5m/s=2m/s;
(2)从A到C过程,由动能定理得:
-mgR(1+cosθ)=$\frac{1}{2}$mvC2-$\frac{1}{2}$mvA2,
在C点,由牛顿第二定律得:mg+F=m$\frac{{v}_{C}^{2}}{R}$,
解得:F=8N,由牛顿第三定律得,
小球对轨道的压力大小F′=F=8N,方向:竖直向上;
(3)小球恰好能够经过最高点C,在C点,
由牛顿第二定律得:mg=m$\frac{v{′}_{C}^{2}}{R}$,
从A到C过程,由动能定理得:
-mgR(1+cosθ)-W=$\frac{1}{2}$mv′C2-$\frac{1}{2}$mvA2,
解得,克服摩擦力做功:W=2J;
答:(1)小球做平抛运动的初速度v0为2m/s,方向:水平向右.
(2)小球到达圆弧最高点C时对轨道的压力大小为8N,方向:竖直向上.
(3)若圆弧轨道粗糙,小球恰好能够经过最高点C,此过程小球克服摩擦力所做的功为2J.
点评 本题是动量守恒定律、平抛运动和圆周运动相结合的典型题目,除了运用动量守恒定律、平抛运动和圆周运动的基本公式外,求速度的问题,动能定理不失为一种好的方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.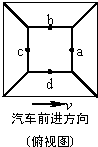 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )| A. | Ta=Tb=Td=Tc,Ea>Eb=Ed>Ec | B. | Ta=Tb=Td=Tc,Ea=Eb=Ed=Ec | ||
| C. | Ta<Tb=Td<Tc,Ea>Eb=Ed>Ec | D. | Ta<Tb=Td<Tc,Ea=Eb=Ed=Ec |
20.小球A从高为H=40m的塔顶自由下落,同时小球B自塔底以速度v0=30m/s竖直上抛,若A、B两球在同一直线上运动,关于两球相遇的位置,下列说法正确的是( )
| A. | 两球在B球上升过程中相遇 | B. | 两球在B球下降过程中相遇 | ||
| C. | 两球在B球运动的最高点相遇 | D. | 两球在空中没有相遇 |
17.下列说法正确的是( )
| A. | 物体所带的电荷量可以是任意实数 | |
| B. | 电场线就是带电粒子只受电场力时的运动轨迹 | |
| C. | 在导体中,只要自由电荷在运动就一定会形成电流 | |
| D. | 磁极与磁极间的相互作用是通过磁场产生的 |
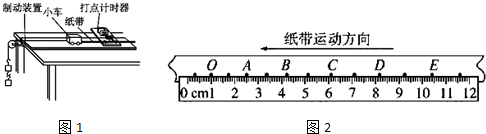
7.某实验小组采用如图所示的装置探究功与速度变化的关系,图中小车中可放置砝码,实验中,小车碰到制动装置时,钩码尚未到达地面,打点针时器工作频率为50Hz.
(1)实验的部分步骤如下:
①在小车中放入砝码,把纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
②将小车停在打点计时器附近,BC小车拖动纸带,打点计时器在纸带上打下一系列点,A;(注意:请选择合适的选项填入上面的横线上A.关闭打点计时器 B.先接通电 C.再释放小车)
③改变钩码或小车中砝码的数量,更换纸带,重复②的操作.
(2)如图是钩码质量为0.03kg、砝码质量为0.02kg时得到的一条纸带,在纸带上选择起始点O及A、B、C、D和E五个计数点,可获得各计数点到O的距离x及对应时刻小车的瞬时速度v,请将C点的测量结果填在表中的相应位置.

(1)实验的部分步骤如下:
①在小车中放入砝码,把纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
②将小车停在打点计时器附近,BC小车拖动纸带,打点计时器在纸带上打下一系列点,A;(注意:请选择合适的选项填入上面的横线上A.关闭打点计时器 B.先接通电 C.再释放小车)
③改变钩码或小车中砝码的数量,更换纸带,重复②的操作.
(2)如图是钩码质量为0.03kg、砝码质量为0.02kg时得到的一条纸带,在纸带上选择起始点O及A、B、C、D和E五个计数点,可获得各计数点到O的距离x及对应时刻小车的瞬时速度v,请将C点的测量结果填在表中的相应位置.
| 测量点 | x/cm | v/(m•s-1) |
| O | 0.00 | 0.35 |
| A | 1.51 | 0.40 |
| B | 3.20 | 0.45 |
| C | 5.10 | 0.49 |
| D | 7.15 | 0.53 |
| E | 9.41 | 0.60 |
 如图所示,用不可伸长的细线悬挂一质量为M=1kg的小木块,木块处于静止状态.现有一质量为m=0.01kg的子弹以初速度v0=300m/s自左方水平地射穿木块,木块上升的最大高度h=0.2m,求:
如图所示,用不可伸长的细线悬挂一质量为M=1kg的小木块,木块处于静止状态.现有一质量为m=0.01kg的子弹以初速度v0=300m/s自左方水平地射穿木块,木块上升的最大高度h=0.2m,求:
 在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2,螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.闭合开关,在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化.电路中电流稳定后电容器两板间的电压是0.6V,下极板带正电.
在如图甲所示的电路中,螺线管匝数n=1500匝,横截面积S=20cm2,螺线管导线电阻r=1.0Ω,R1=4.0Ω,R2=5.0Ω,C=30μF.闭合开关,在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化.电路中电流稳定后电容器两板间的电压是0.6V,下极板带正电.