题目内容
20.从20m高的平台边缘有一小球A自由落下,此时恰有一小球B在A球下方从地面上以20m/s的初速度竖直上抛(不计空气阻力g 取10m/s2).求:(1)经过多长时间小球A落地;
(2)小球B上升的最大高度为多少;
(3)经过多长时间两球在空中相遇.
分析 (1)A做自由落体运动,由自由落体位移时间公式,可求下落时间.
(2)B做加速为-g的匀变速运动,末速度为0,由速度位移关系式可求上升高度.
(3)两球相遇时位移之和为20m,由匀变速规律可得时间.
解答 解:
(1)A做自由落体运动,则:
${h}_{1}=\frac{1}{2}g{t}_{1}^{2}\\;\\;\$
解得:
${t}_{1}=\sqrt{\frac{2{h}_{1}}{g}}=\sqrt{\frac{2×20}{10}}=2s$.
(2)B做加速为-g的匀变速运动,末速度为0,则:
${v}_{0}^{2}=2g{h}_{2}$
解得:
${h}_{2}=\frac{{20}^{2}}{2×10}=20m$.
(3)设经历时间t,两球在空中相遇:
相遇时:
h1=hA+hB
=$\frac{1}{2}g{t}^{2}+{v}_{0}t-\frac{1}{2}g{t}^{2}$
=v0t
解得:
$t=\frac{h}{{v}_{0}}=\frac{20}{20}=1s$.
答:
(1)经过2s小球A落地;
(2)小球B上升的最大高度为20m;
(3)经过1s两球在空中相遇.
点评 解决本题的关键知道两物体在空中相碰,两物体的位移之和等于两球的初始距离,这是相遇类问题的特征.

练习册系列答案
相关题目
10. 如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )
如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )
 如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )
如图所示,试管中有一根弹簧,一个质量为m的小球压在弹簧上.开始时手握住试管处于静止状态,现在突然放手,则小球在开始阶段的运动,在地面上的人看来是( )| A. | 自由落体运动 | B. | 向上升起一定高度后落下 | ||
| C. | 向下做加速度小于g的运动 | D. | 向下做加速度大于g的运动 |
11.物体受到几个恒力的作用而处于平衡状态,若再对物体施加一个恒力,则物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | ||
| C. | 非匀变速曲线运动 | D. | 匀变速曲线运动 |
15.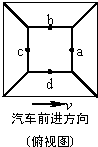 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )| A. | Ta=Tb=Td=Tc,Ea>Eb=Ed>Ec | B. | Ta=Tb=Td=Tc,Ea=Eb=Ed=Ec | ||
| C. | Ta<Tb=Td<Tc,Ea>Eb=Ed>Ec | D. | Ta<Tb=Td<Tc,Ea=Eb=Ed=Ec |
12.一个做匀加速直线运动的物体的加速度是3m/s2,这意味着( )
| A. | 该物体在任1 s末的速度是该秒初速度的3倍 | |
| B. | 该物体在任1 s末的速度比该秒的初速度大3 m/s | |
| C. | 该物体在第1 s末的速度为3 m/s | |
| D. | 该物体在任1 s初的速度比前1 s末的速度大3 m/s |
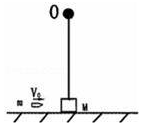 如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.
如图所示,在光滑的水平面上放着一个质量为M=0.39kg的木块(可视为质点),在木块正上方有一个固定悬点O,在悬点O和木块之间连接一根长度为0.4m的轻绳(轻绳不可伸长且刚好被拉直).有一颗质量为m=0.01kg的子弹以水平速度V0射入木块并留在其中(作用时间极短),g取10m/s2,要使木块能绕O点在竖直平面内做圆周运动,求:子弹射入的最小速度.