题目内容
6.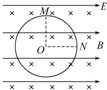 如图所示,半径为R的光滑绝缘环竖直置于彼此正交的水平匀强电场和垂直纸面向里的匀强磁场中,磁感应强度为B,今有一质量为m、带电荷量为+q的空心小球穿在环上,已知小球所受电场力和重力大小相等,则当小球由静止开始从环顶M下滑到与圆心等高的N点时,小球给环的压力大小为多少?
如图所示,半径为R的光滑绝缘环竖直置于彼此正交的水平匀强电场和垂直纸面向里的匀强磁场中,磁感应强度为B,今有一质量为m、带电荷量为+q的空心小球穿在环上,已知小球所受电场力和重力大小相等,则当小球由静止开始从环顶M下滑到与圆心等高的N点时,小球给环的压力大小为多少?
分析 根据动能定理求出小球到达N点时的速度,再根据向心力公式求出小球在N的弹力,即小球对环的压力
解答 解:设环滑到N点时速度为v,由动能定理有
mgR+qER=$\frac{1}{2}$mv2-0,
而qE=mg,可得v=$\sqrt{4gR}$.
环在N点时,设环受到压力为FN,则有
${F}_{N}^{\;}-qE-qvB=m\frac{{v}_{\;}^{2}}{R}$,
得:${F}_{N}^{\;}=qE+qvB+m\frac{{v}_{\;}^{2}}{R}=5mg+2qB\sqrt{gR}$
根据牛顿第三定律${F}_{N}^{′}=5mg+2qB\sqrt{gR}$
答:小球给环的压力大小为$5mg+2qB\sqrt{gR}$
点评 本题考查动能定理的应用,掌握牛顿第二、三定律的内容,理解向心力的表达式,关键是受力分析和运动过程分析,运用合适的规律进行解题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
1.如图所示为物体分子势能与分子间距离之间的关系,下列判断正确的是( )
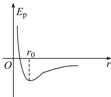

| A. | 当r<r0时,r越小,则分子势能Ep越大 | |
| B. | 当r>r0时,r越小,则分子势能Ep越大 | |
| C. | 当r=r0时,分子势能Ep最小 | |
| D. | 当r→∞时,分子势能Ep最小 |
11.物体受到几个恒力的作用而处于平衡状态,若再对物体施加一个恒力,则物体不可能做( )
| A. | 匀加速直线运动 | B. | 匀减速直线运动 | ||
| C. | 非匀变速曲线运动 | D. | 匀变速曲线运动 |
15.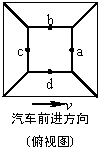 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
 沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )
沿平直公路匀速行驶的汽车上,固定着一个正四棱台,其上下台面水平,如图为俯视示意图.在顶面上四边的中点a、b、c、d 沿着各斜面方向,同时相对于正四棱台无初速释放4 个相同小球.设它们到达各自棱台底边分别用时Ta、Tb、Tc、Td,到达各自棱台底边时相对于地面的机械能分别为Ea、Eb、Ec、Ed(取水平地面为零势能面,忽略斜面对小球的摩擦力).则有( )| A. | Ta=Tb=Td=Tc,Ea>Eb=Ed>Ec | B. | Ta=Tb=Td=Tc,Ea=Eb=Ed=Ec | ||
| C. | Ta<Tb=Td<Tc,Ea>Eb=Ed>Ec | D. | Ta<Tb=Td<Tc,Ea=Eb=Ed=Ec |
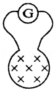 如图所示,在物理实验中,常用“冲击式电流计”来测定通过某闭合电路的电荷量.探测器线圈和冲击电流计串联后,又能测定磁场的磁感应强度.已知线圈匝数为n,面积为S,线圈与冲击电流计组成的回路电阻为R.把线圈放在匀强磁场时,开始时线圈与磁场方向垂直,现将线圈翻转180°,冲击式电流计测出通过线圈的电荷量为q,由此可知,被测磁场的磁感应强度B=$\frac{qR}{2nS}$.
如图所示,在物理实验中,常用“冲击式电流计”来测定通过某闭合电路的电荷量.探测器线圈和冲击电流计串联后,又能测定磁场的磁感应强度.已知线圈匝数为n,面积为S,线圈与冲击电流计组成的回路电阻为R.把线圈放在匀强磁场时,开始时线圈与磁场方向垂直,现将线圈翻转180°,冲击式电流计测出通过线圈的电荷量为q,由此可知,被测磁场的磁感应强度B=$\frac{qR}{2nS}$.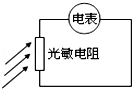 光敏电阻是用半导体材料制成的.如图所示,将一个光敏电阻与多用电表联成一电路,此时选择开关放在欧姆档,照射在光敏电阻上的光强逐渐增大,则欧姆表指针的偏转角度变大(填“变大”、“变小”或“不变”).若将选择开关放在电流挡,同样增大照射光强度,则指针偏转角度不变.(填“变大”、“变小”或“不变”).
光敏电阻是用半导体材料制成的.如图所示,将一个光敏电阻与多用电表联成一电路,此时选择开关放在欧姆档,照射在光敏电阻上的光强逐渐增大,则欧姆表指针的偏转角度变大(填“变大”、“变小”或“不变”).若将选择开关放在电流挡,同样增大照射光强度,则指针偏转角度不变.(填“变大”、“变小”或“不变”). 某居住地A位于某山脉的一边,山脉的另一边P处建有一无线电波发射站,如图所示.该发射站可发送频率为400kHz的中波和频率为400MHz的微波,已知无线电波在空气中的传播速度都为3×108 m/s,求:
某居住地A位于某山脉的一边,山脉的另一边P处建有一无线电波发射站,如图所示.该发射站可发送频率为400kHz的中波和频率为400MHz的微波,已知无线电波在空气中的传播速度都为3×108 m/s,求: