Question

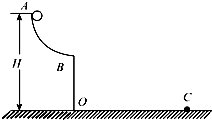
如图所示，在光滑水平面上竖直固定一半径为R=0.5m的光滑半圆槽轨道，其底端恰与水平面相切．质量为m的小球以大小为v₀=5m/s的初速度经半圆槽轨道最低点B滚上半圆槽，小球恰能通过最高点C后落回到水平面上的A点．（不计空气阻力，重力加速度为g）求：
（1）小球通过B点时对半圆槽的压力大小；
（2）AB两点间的距离．

Answer 1

（1）对小球在B点时受力分析，根据牛顿第二定律：
F-mg=m

v02

R

得：F=60m
根据牛顿第三定律有：F′=F=60m；
（2）小球在C点时：mg=m

vc2

R

得：v_c=

gR

=

5

m/s
由C到A做平抛运动：2R=

1

2

gt²
得：t=

4R g

=

2 10

s
x=v_ct=

5

×

2 10

=1m
答：（1）小球通过B点时对半圆槽的压力大小为60m；
（2）AB两点间的距离为1m．