题目内容
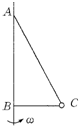
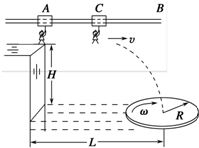
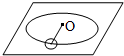
如图所示的试管内封有一定质量的气体,静止时气柱长为L0,大气压强为P0,当试管绕竖直轴以角速度ω在水平面匀速转动时气柱长变为L,其他尺寸如图2-6所示,求转动时的气体压强.(设温度不变,管截面积为S,水银密度为ρ)


选取水银柱为研究对象,转动所需向心力由液柱两侧气体压力差提供,
根据牛顿第二定律,则有:
F向=(P-P0)S=mω2RS
而m=ρL1S.
由几何关系,则有R=L2+(L0-L)+
因此P=P0+ρL1ω2(L2+L0-L+
).
答:转动时的气体压强P=P0+ρL1ω2(L2+L0-L+
).
根据牛顿第二定律,则有:
F向=(P-P0)S=mω2RS
而m=ρL1S.
由几何关系,则有R=L2+(L0-L)+
| L1 |
| 2 |
因此P=P0+ρL1ω2(L2+L0-L+
| L1 |
| 2 |
答:转动时的气体压强P=P0+ρL1ω2(L2+L0-L+
| L1 |
| 2 |

练习册系列答案
相关题目