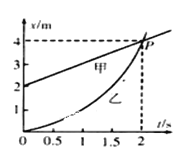
��Ŀ����
����Ŀ����ͼ��ʾ���ֲ�ˮƽ����뾶ΪR=9.8m�Ĺ⻬ ![]() Բ�����ƽ�����ӣ�����Ϊm��С����A��ˮƽ����F=1.5mg�������´�ˮƽ�����ij�������˶�����F����t1=2s��ȥ��С����A�����˶�t2=2s���뾲ֹ��Բ������˵���һС����B����������ײ������С����B����Բ��������������߶�Ϊh=
Բ�����ƽ�����ӣ�����Ϊm��С����A��ˮƽ����F=1.5mg�������´�ˮƽ�����ij�������˶�����F����t1=2s��ȥ��С����A�����˶�t2=2s���뾲ֹ��Բ������˵���һС����B����������ײ������С����B����Բ��������������߶�Ϊh= ![]() ����֪С������ˮƽ���Ķ�Ħ��������=0.5���������ٶ�g=9.8m/s2 ��
����֪С������ˮƽ���Ķ�Ħ��������=0.5���������ٶ�g=9.8m/s2 �� 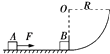
����С����A��С����B��ײǰ˲����ٶ�v0��
��������B������M��
���𰸡��⣺������A��ײǰ�˶����̣��涨����Ϊ�������ɶ����������У�
Ft1����mg��t1+t2��=mv0��0
��ã�
v0=9.8m/s
����ײ��A��B�ٶȷֱ�Ϊv1��v2���ɻ�е���غ㶨�ɣ��У�
Mgh= ![]()
��ã�
v2=4.9m/s
���ڵ�����ײ���̣��������غ㶨�ɣ��У�
![]()
�ɶ����غ㶨�ɣ��У�
mv0=mv1+Mv2
������ã�
M=3m
��С����A��С����B��ײǰ˲����ٶ�v0Ϊ9.8m/s��С����B������MΪ3m
��������������A��ײǰ�˶������и�����������ʱ�������֪�ģ����Ը��ݶ���������ʽ���ĩ�ٶȣ���С����B��Բ��������˶����̻�е���غ㣬����A��B��ײ�����ǵ�����ײ�����������غ㶨�ɺͶ����غ㶨�ɷֱ���ʽ�����������⼴�ɣ�
�����㾫�����������⣬������Ҫ�˽�ܶ������ۺ�Ӧ��(Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ��)����Ҫ���ն����غ㶨��(�����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ���)�����֪ʶ���Ǵ���Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�