��Ŀ����
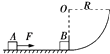
����Ŀ����ͼ����ʾ��������У��뾶ΪR��Բ�������ڴ�����ǿ�ų����ų�����ֱֽ�����⣮�ڴų������һ��ƽ�н�����M��N����������ҲΪR���峤ΪL�����������O1O2��ų���Բ��O��ͬһֱ���ϣ�����O1�������ӷ���Դ���������ٶ�v0�����������O1O2��������Ϊq������Ϊm�Ĵ���������ӣ�����������������MN���岻�ӵ�ѹʱ�����Ӿ��ų�ƫת��ǡ�ô�Բ��O�����·�P���뿪�ų�������M��N������ͼ����ʾ�����ѹUMN �� �����ѹ������Ϊ ![]() ��t=0ʱ�����������ǡ������N���Ҳ��������
��t=0ʱ�����������ǡ������N���Ҳ��������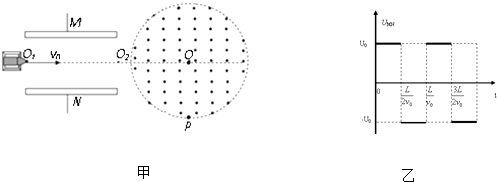
��1����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�С
��2�������ѹ��ѹU0��ֵ
��3���������ڴų����˶���������ʱ��ֱ�Ϊt1��t2 �� �����ǵIJ�ֵ��tΪ���
���𰸡�
��1���⣺��UMN=0ʱ������O2O3��������ų��켣��ͼ��O1������뾶ΪR1��
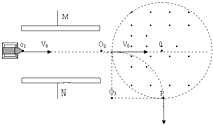
�ɼ��ι�ϵ�ã�R1=R
���� ![]()
��ã� ![]() ��
��
����ǿ�ų��ĴŸ�Ӧǿ��B�Ĵ�СΪ ![]()
��2���⣺��t=0ʱ�������������㣺 ![]() ��
��
��ã� ![]() ��
��
�𣺽����ѹ��ѹU0��ֵΪ ![]()
��3���⣺��������֪�������Ӿ��糡�����ٶ���Ϊv0��
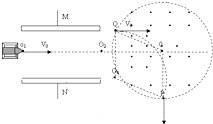
�� ![]() ��k=0��1��2��3������ʱ�������������M��ƽ������ų��켣���04��ƫת��Ϊ����
��k=0��1��2��3������ʱ�������������M��ƽ������ų��켣���04��ƫת��Ϊ����
�ɼ���֪ʶ��֪�ı���QOPO4Ϊ���Σ��ʦ�=120��
![]() ��
��
�� ![]() ��k=0��1��2��3������ʱ�������������N��ƽ������ų��켣���05 ƫת��Ϊ�£�
��k=0��1��2��3������ʱ�������������N��ƽ������ų��켣���05 ƫת��Ϊ�£�
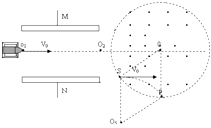
�ɼ���֪ʶ��֪SOPO5Ϊ���Σ��ʦ�=60��
![]() ��
��
�� ![]()
�� ![]() ��
��
���������ڴų����˶���������ʱ��ֱ�Ϊt1��t2�������ǵIJ�ֵ��tΪ ![]() ��
��
����������1�����ݼ��ι�ϵ��������ڴų����˶��Ĺ���뾶����ϰ뾶��ʽ�����ǿ�ų��ĴŸ�Ӧǿ�ȴ�С����2������ƫתλ�ƵĴ�С�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ��������ѹU0��ֵ����3���������Ӿ��糡�����ٶ���Ϊv0�����������ڴų����˶�Բ�Ľ�������Сʱ�Ĺ켣ͼ��������ڹ�ʽ������⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�