题目内容
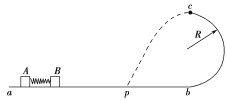
【题目】如图所示,一条轨道固定在竖直平面内,粗糙的ab段水平,bcd段光滑,cd段是以O为圆心,R为半径的一小段圆弧,末端d水平,可视为质点的物块A和B紧靠在一起,静止于b处,A的质量是B的3倍.两物块在足够大的内力作用下突然分离,分别向左、右沿轨道运动.B运动到d点时轨道对B的支持力大小等于B所受重力的![]() ,A与ab段的动摩擦因数为μ,重力加速度为g,不计空气阻力.求:
,A与ab段的动摩擦因数为μ,重力加速度为g,不计空气阻力.求:

(1)物块B离开d后落点到O的距离;
(2)物块A、B在b点刚分离时,物块B的速度大小;
(3)物块A滑行的最大距离s.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设物块B的质量为mB,在d点时速度为v,轨道对它的支持力为FN,由牛顿运动定律
mBg-FN=![]() ,FN=
,FN=![]()
解得
v =![]()
物块B离开d后做平抛运动,则:
R=![]() ,x=vt
,x=vt
解得落点到O的距离为
x=![]()
(2)设物块B在b点刚分开时的速度为vB,由机械能守恒有:
![]()
解得
vB=![]()
(3)设物块B分离时速度方向为正方向,物块A的质量为mA,A和B分离时的速度为vA,由动量守恒定律
mAvA+mBvB=0,mA=3mB
物块A和B分离后,物块A做匀减速直线运动滑行的最大距离为s,由动能定理得
-μmAgs=0-![]()
解得
s=![]()

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目