题目内容
【题目】如图所示，半径为R的竖直光滑半圆轨道bc与水平光滑轨道ab在b点连接，开始时可视为质点的物体A和B静止在ab上，A、B之间压缩有一处于锁定状态的轻弹簧(弹簧与A，B不连接)．某时刻解除锁定，在弹力作用下A向左运动，B向右运动，B沿轨道经过c点后水平抛出，落点p与b点间距离为2R.已知A质量为2m，B质量为m，重力加速度为g，不计空气阻力，求：
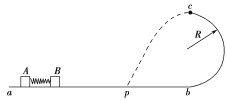
(1)B经c点抛出时速度的大小？
(2)B经b时速度的大小？
(3)锁定状态的弹簧具有的弹性势能？
【答案】(1) 
(2) 
(3) 3.75mgR
【解析】
(1)B平抛运动过程竖直方向有2R＝
gt2，水平方向：2R＝vct，解得：vc＝.
(2)B从b到c，由机械能守恒定律得
解得：vb＝
(3)设完全弹开后，A的速度为va，弹簧回复原长过程中A与B组成系统动量守恒，2mva－mvb＝0，解得：va＝vb＝
，由能量守恒定律，得弹簧弹性势能：
解得：Ep＝3.75mgR.
练习册系列答案
相关题目
