题目内容
5.如图所示,小球B与一轻质弹簧相连,并静止在足够长的光滑水平面上,小球A以某一速度与轻质弹簧正碰.小球A与弹簧分开后,小球B的速度为v.碰撞过程中,当两个小球与弹簧组成的系统动能最小时,小球B的速度多大?
分析 当系统动能最小时,弹簧压缩至最短,两球具有共同速度,根据系统的动量守恒和机械能守恒列式求解.
解答 解:当系统动能最小时,弹簧压缩至最短,两球具有共同速度v共.设小球A、B的质量分别为m1、m2,碰撞前后A的速度分别为v01、v1.取向右为正方向,由系统动量守恒和能量守恒有:
m1v01=m1v1+m2v…①
$\frac{1}{2}$m1v012=$\frac{1}{2}$m1v12+$\frac{1}{2}$m2v2…②
联立①②解得:m1v01=$\frac{{m}_{1}+{m}_{2}}{2}$v…③
碰撞过程任一时刻系统动量守恒,故:m1v01=(m1+m2)v共…④
将③式代入④式解得:v共=$\frac{v}{2}$…⑤
即系统动能最小时,小球B的速度为$\frac{v}{2}$.
答:系统动能最小时,小球B的速度为$\frac{v}{2}$.
点评 本题是含有弹簧的问题,要分析物体的运动过程,知道系统动能最小的条件:速度相同,抓住系统的动量守恒和机械能守恒进行研究.

练习册系列答案
相关题目
14.关于矢量和标量的说法中正确的是( )
| A. | 平均速度、瞬时速度和加速度都是矢量,速率、平均速率、时间和质量都是标量 | |
| B. | 比较矢量大小,只要比较值的大小,而比较标量的大小要带(+、-)符号进行 | |
| C. | 矢量的合成满足平行四边形法则,标量的合成只要代数加减即可 | |
| D. | 矢量和标量没有严格的区别,同一个物理量有时是矢量,有时是标量 |
13. 如图所示,在“嫦娥”探月工程中,设月球半径为R,月球表面的重力加速度为g0.飞船在半径为4R的圆形轨道Ⅰ上运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时,再次点火进入近月轨道Ⅲ绕月做圆周运动,则( )
如图所示,在“嫦娥”探月工程中,设月球半径为R,月球表面的重力加速度为g0.飞船在半径为4R的圆形轨道Ⅰ上运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时,再次点火进入近月轨道Ⅲ绕月做圆周运动,则( )
 如图所示,在“嫦娥”探月工程中,设月球半径为R,月球表面的重力加速度为g0.飞船在半径为4R的圆形轨道Ⅰ上运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时,再次点火进入近月轨道Ⅲ绕月做圆周运动,则( )
如图所示,在“嫦娥”探月工程中,设月球半径为R,月球表面的重力加速度为g0.飞船在半径为4R的圆形轨道Ⅰ上运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时,再次点火进入近月轨道Ⅲ绕月做圆周运动,则( )| A. | 飞船在轨道Ⅲ的运行速率约等于$\sqrt{{g}_{0}R}$ | |
| B. | 飞船在轨道Ⅰ经A处的速率小于在轨道Ⅱ经A处的速度 | |
| C. | 飞船在A处重力加速度小于在B处重力加速度 | |
| D. | 飞船在轨道Ⅰ、轨道Ⅱ、轨道Ⅲ上运行的周期有T1>T2>TIII |
20. 如图所示,在足够高处有两个小球A、B处在同一竖直线上,两球相距L,用长为2L的细线连接,现同时将A、B两个小球以相反方向的初速度v1、v2水平抛出,则从抛出后至细线拉直所需的时间为( )
如图所示,在足够高处有两个小球A、B处在同一竖直线上,两球相距L,用长为2L的细线连接,现同时将A、B两个小球以相反方向的初速度v1、v2水平抛出,则从抛出后至细线拉直所需的时间为( )
 如图所示,在足够高处有两个小球A、B处在同一竖直线上,两球相距L,用长为2L的细线连接,现同时将A、B两个小球以相反方向的初速度v1、v2水平抛出,则从抛出后至细线拉直所需的时间为( )
如图所示,在足够高处有两个小球A、B处在同一竖直线上,两球相距L,用长为2L的细线连接,现同时将A、B两个小球以相反方向的初速度v1、v2水平抛出,则从抛出后至细线拉直所需的时间为( )| A. | $\frac{L}{{v}_{1}+{v}_{2}}$ | B. | $\frac{\sqrt{2}L}{{v}_{1}+{v}_{2}}$ | C. | $\frac{\sqrt{3}L}{{v}_{1}+{v}_{2}}$ | D. | $\frac{2L}{{v}_{1}+{v}_{2}}$ |
10.在不计地球自转的情况下,一个物体在地球表面所受的重力为G,在距离地面高度为地球半径的位置,物体所受地球的引力大小为( )
| A. | $\frac{G}{2}$ | B. | $\frac{G}{3}$ | C. | $\frac{G}{4}$ | D. | $\frac{G}{9}$ |
14.一质量为2kg的物块在水平牵引力的作用下做直线运动,v-t图象如图1所示,物块与水平地面间的动摩擦因数为0.4.下列说法正确的是( )
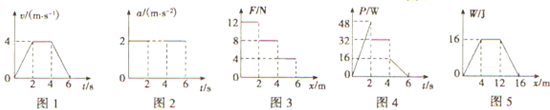

| A. | 图2 表示物块的加速度随时间的变化关系 | |
| B. | 图3 表示水平牵引力随位移的变化关系 | |
| C. | 图4 表示水平牵引力功率随时间的变化关系 | |
| D. | 图5 表示合力对物块做的功随位移的变化关系 |
15.位于地球赤道上随地球自转的物体和地球的同步通信卫星均在赤道平面上绕地心做匀速圆周运动.已知地球同步通信卫星轨道半径为r,地球半径为R,第一宇宙速度为v.仅利用以上己知条件能求出( )
| A. | 地球的自转周期 | B. | 地球的质量 | ||
| C. | 随地球自转的物体的线速度 | D. | 万有引力常量 |
 如图所示是电视机电源部分的滤波装置,当输入端输入含有直流成分、交流低频成分的电流后,能在输出端得到较稳定的直流电,试分析其工作原理及各电容和电感的作用.
如图所示是电视机电源部分的滤波装置,当输入端输入含有直流成分、交流低频成分的电流后,能在输出端得到较稳定的直流电,试分析其工作原理及各电容和电感的作用. 最新研究表明,中子内有一个电荷量为+$\frac{2}{3}$e的上夸克和两个电荷量为-$\frac{1}{3}$e的下夸克,一简单模型是三个夸克都在半径为r的同一圆周上,如图所示.试在图中准确画出,左边一个-$\frac{1}{3}$e夸克,所受另外两个夸克粒子对其的静电作用力以及静电力的合力.(作图时,力矢量的相对关系要求准确)
最新研究表明,中子内有一个电荷量为+$\frac{2}{3}$e的上夸克和两个电荷量为-$\frac{1}{3}$e的下夸克,一简单模型是三个夸克都在半径为r的同一圆周上,如图所示.试在图中准确画出,左边一个-$\frac{1}{3}$e夸克,所受另外两个夸克粒子对其的静电作用力以及静电力的合力.(作图时,力矢量的相对关系要求准确)