题目内容
17. 最新研究表明,中子内有一个电荷量为+$\frac{2}{3}$e的上夸克和两个电荷量为-$\frac{1}{3}$e的下夸克,一简单模型是三个夸克都在半径为r的同一圆周上,如图所示.试在图中准确画出,左边一个-$\frac{1}{3}$e夸克,所受另外两个夸克粒子对其的静电作用力以及静电力的合力.(作图时,力矢量的相对关系要求准确)
最新研究表明,中子内有一个电荷量为+$\frac{2}{3}$e的上夸克和两个电荷量为-$\frac{1}{3}$e的下夸克,一简单模型是三个夸克都在半径为r的同一圆周上,如图所示.试在图中准确画出,左边一个-$\frac{1}{3}$e夸克,所受另外两个夸克粒子对其的静电作用力以及静电力的合力.(作图时,力矢量的相对关系要求准确)
分析 每一个夸克都受到其他两个夸克的库仑力作用,根据库仑定律和力的合成求解.
解答 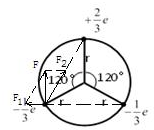 解:三个夸克都在半径为r的同一圆周,形成了等边三角形,
解:三个夸克都在半径为r的同一圆周,形成了等边三角形,
电荷量为-$\frac{1}{3}$e的下夸克受到另一个电荷量为-$\frac{1}{3}$e的下夸克的库仑斥力F1
和电荷量为+$\frac{2}{3}$e的上夸克库仑引力F2.
根据库仑定律得:F1=$\frac{1}{2}$F2
根据库仑定律,则有:F1=$\frac{k\frac{e}{3}×\frac{e}{3}}{(\sqrt{3}r)^{2}}$=$\frac{k{e}^{2}}{27{r}^{2}}$,F2=$\frac{2k{e}^{2}}{27{r}^{2}}$
根据力的合成得F1和F2的合力方向竖直向上,且合力的大小为:F=$\frac{\sqrt{3}k{e}^{2}}{27{r}^{2}}$.
答:所受另外两个夸克粒子对其的静电作用力分别为$\frac{k{e}^{2}}{27{r}^{2}}$与$\frac{2k{e}^{2}}{27{r}^{2}}$,以及静电力的合力$\frac{\sqrt{3}k{e}^{2}}{27{r}^{2}}$.
点评 本题电场的叠加问题,要利用对称性.对于两个下夸克场强的合成可利用力的合成进行类比,解决该题关键要根据库仑定律以及矢量的合成完成.

练习册系列答案
相关题目
7.如图所示为LC振荡电路,当开关S打向右边发生振荡后,下列说法中正确的是( )


| A. | 振荡电流达到最大值时,电容器上的带电量为零 | |
| B. | 振荡电流达到最大值时,磁场能最大 | |
| C. | 振荡电流为零时,电场能为零 | |
| D. | 振荡电流相邻两次为零的时间间隔等于振荡周期的一半 |
8. 如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
 如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )| A. | 推力F增大 | B. | 地面对小球B的弹力不变 | ||
| C. | 两个小球之间的距离减小 | D. | 竖直墙面对小球A的弹力增大 |
12.在做“研究平抛运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是( )
| A. | 秒表 | B. | 坐标纸 | C. | 重锤线 | D. | 弹簧秤 |
2.如图所示为甲、乙两物体从同一地点沿直线向同一方向运动的v-t图象,则( )


| A. | 甲、乙两物体在4s末相距最远 | |
| B. | 甲、乙两物体在4s末相遇λ | |
| C. | 前4s内甲物体的速度总是大于乙的速度 | |
| D. | 甲、乙两物体在2.5s末相距最远 |
9.用图甲所示实验装置研究光电效应现象,分别用a,b,c三束光照射光电管阴极,得到光电管两端的电压与相应的光电流的关系如图乙所示,其中a,c两束光照射时对应的遏止电压相同,均为Uc1,根据你所学的相关理论下列论述正确的是( )


| A. | a,c两束光的光强相同 | |
| B. | a,c两束光的频率相同 | |
| C. | b光束的光的波长最短 | |
| D. | a光束照射时光电管发出的光电子的最大初动能最大 | |
| E. | b光束光子的动量最大 |
6.一物体自t=0时开始做直线运动,其速度图线如图所示.下列选项正确的是( )

| A. | 在0~6s内,物体经过的路程为40m | B. | 在0~6s内,物体离出发点最远为30m | ||
| C. | 在0~4s内,物体的平均速率为8m/s | D. | 5~6s内,物体所受的合外力做负功 |
10. 如图所示,高为h光滑水平平台上有一个质量为m的物块,在绝缘水平面有一个质量也为m、电荷量为q的带正电的小球,平台下面有水平向右电场强度为E的匀强电场,小球用跨过定滑轮的绳子向右拉动物块,且小球始终没有离开绝缘水平面,不计一切摩擦.当小球从平台的边缘处由静止向右前进位移h时,物块的速度v是( )
如图所示,高为h光滑水平平台上有一个质量为m的物块,在绝缘水平面有一个质量也为m、电荷量为q的带正电的小球,平台下面有水平向右电场强度为E的匀强电场,小球用跨过定滑轮的绳子向右拉动物块,且小球始终没有离开绝缘水平面,不计一切摩擦.当小球从平台的边缘处由静止向右前进位移h时,物块的速度v是( )
 如图所示,高为h光滑水平平台上有一个质量为m的物块,在绝缘水平面有一个质量也为m、电荷量为q的带正电的小球,平台下面有水平向右电场强度为E的匀强电场,小球用跨过定滑轮的绳子向右拉动物块,且小球始终没有离开绝缘水平面,不计一切摩擦.当小球从平台的边缘处由静止向右前进位移h时,物块的速度v是( )
如图所示,高为h光滑水平平台上有一个质量为m的物块,在绝缘水平面有一个质量也为m、电荷量为q的带正电的小球,平台下面有水平向右电场强度为E的匀强电场,小球用跨过定滑轮的绳子向右拉动物块,且小球始终没有离开绝缘水平面,不计一切摩擦.当小球从平台的边缘处由静止向右前进位移h时,物块的速度v是( )| A. | $v=\sqrt{\frac{qEh}{m}}$ | B. | $v=\sqrt{\frac{2qEh}{3m}}$ | C. | $v=\sqrt{\frac{4qEh}{3m}}$ | D. | $v=\sqrt{\frac{2qEh}{m}}$ |
