题目内容
20. 如图所示,在足够高处有两个小球A、B处在同一竖直线上,两球相距L,用长为2L的细线连接,现同时将A、B两个小球以相反方向的初速度v1、v2水平抛出,则从抛出后至细线拉直所需的时间为( )
如图所示,在足够高处有两个小球A、B处在同一竖直线上,两球相距L,用长为2L的细线连接,现同时将A、B两个小球以相反方向的初速度v1、v2水平抛出,则从抛出后至细线拉直所需的时间为( )| A. | $\frac{L}{{v}_{1}+{v}_{2}}$ | B. | $\frac{\sqrt{2}L}{{v}_{1}+{v}_{2}}$ | C. | $\frac{\sqrt{3}L}{{v}_{1}+{v}_{2}}$ | D. | $\frac{2L}{{v}_{1}+{v}_{2}}$ |
分析 两个小球做平抛运动,在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.当细线被拉直时,两个小球间的距离等于2L,根据运动学公式和几何关系求解.
解答 解:设经过时间t细线拉直.根据平抛运动的规律和几何关系可得:
(2L)2=$({v}_{1}t+{v}_{2}t)^{2}$+$(L+\frac{1}{2}g{t}^{2}-\frac{1}{2}g{t}^{2})^{2}$
解得 t=$\frac{\sqrt{3}L}{{v}_{1}+{v}_{2}}$
故选:C
点评 解决本题的关键是抓住隐含的条件,知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
 如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )
如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球,A、B分别处于竖直墙面和水平地面上,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,待两球重新达到平衡时,则两个小球的受力情况与原来相比( )| A. | 推力F增大 | B. | 地面对小球B的弹力不变 | ||
| C. | 两个小球之间的距离减小 | D. | 竖直墙面对小球A的弹力增大 |
15. 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
 如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )
如图所示,中间有孔的物块A套在光滑的竖直杆上,通过滑轮用不可伸长的轻绳将物体拉着匀速向上运动,则关于拉力F及拉力作用点的移动速度v的下列说法正确的是( )| A. | F不变,v不变 | B. | F增大,v减小 | C. | F增大,v增大 | D. | F增大,v不变 |
12.在做“研究平抛运动”实验时,除了木板、小球、斜槽、铅笔、图钉之外,下列器材中还需要的是( )
| A. | 秒表 | B. | 坐标纸 | C. | 重锤线 | D. | 弹簧秤 |
9.用图甲所示实验装置研究光电效应现象,分别用a,b,c三束光照射光电管阴极,得到光电管两端的电压与相应的光电流的关系如图乙所示,其中a,c两束光照射时对应的遏止电压相同,均为Uc1,根据你所学的相关理论下列论述正确的是( )


| A. | a,c两束光的光强相同 | |
| B. | a,c两束光的频率相同 | |
| C. | b光束的光的波长最短 | |
| D. | a光束照射时光电管发出的光电子的最大初动能最大 | |
| E. | b光束光子的动量最大 |
10.某实验小组利用下列的实验器材测绘一段某种导电材料的U-I特性曲线.实验器材有:电流表A(0.6A/3A,内阻小于0.1Ω)
电压表V(3V/15V,内阻大于9kΩ)
学生电源E(3V直流电源)
滑动变阻器R(最大阻值为25Ω)
开关K和导线若干.
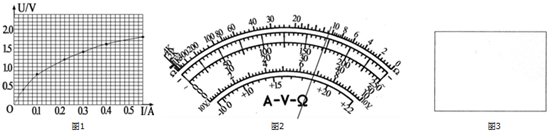
该实验小组大约每隔2分钟测量一组数据,下面是他们记录的实验数据及作出电阻的U-I图线(如图1):
(1)在图3方框内画出实验的电路图.
(2)分析实验画出的U-I图线弯曲的主要原因是:电阻随温度的升高而减小.
(3)分析本实验中在某确定的温度下电阻测量值R测与真实值R真的大小关系,并说明产生此误差的原因.电压表的分流.
(4)该实验小组用多用表的“×10”欧姆挡测试这段材料在常温下的电阻,操作步骤正确,发现表头指针偏转的角度很大.为了准确地进行测量,应换到×1档(只考虑临近档位).如果换档后立即用表笔连接待测电阻进行读数,那么欠缺的步骤是:两表笔直接接触,调节欧姆调零旋钮,使指针指在“0Ω”处,补上该步骤后,表盘的示数如图2所示,则该材料的电阻是11Ω.
电压表V(3V/15V,内阻大于9kΩ)
学生电源E(3V直流电源)
滑动变阻器R(最大阻值为25Ω)
开关K和导线若干.
该实验小组大约每隔2分钟测量一组数据,下面是他们记录的实验数据及作出电阻的U-I图线(如图1):
| 序号 | 电压表示数/V | 电流表示数/A |
| 1 | 0.40 | 0.04 |
| 2 | 0.80 | 0.10 |
| 3 | 1.20 | 0.22 |
| 4 | 1.40 | 0.30 |
| 5 | 1.60 | 0.40 |
| 6 | 1.80 | 0.56 |
(2)分析实验画出的U-I图线弯曲的主要原因是:电阻随温度的升高而减小.
(3)分析本实验中在某确定的温度下电阻测量值R测与真实值R真的大小关系,并说明产生此误差的原因.电压表的分流.
(4)该实验小组用多用表的“×10”欧姆挡测试这段材料在常温下的电阻,操作步骤正确,发现表头指针偏转的角度很大.为了准确地进行测量,应换到×1档(只考虑临近档位).如果换档后立即用表笔连接待测电阻进行读数,那么欠缺的步骤是:两表笔直接接触,调节欧姆调零旋钮,使指针指在“0Ω”处,补上该步骤后,表盘的示数如图2所示,则该材料的电阻是11Ω.

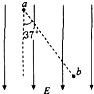 如图所示,a、b是匀强电场中的两点,质子只在电场力作用下,从a点移动到b点的过程中,电场力将做正(选填“正”或“负”)功,质子的速度将增大(选填“增大”或“减小”)
如图所示,a、b是匀强电场中的两点,质子只在电场力作用下,从a点移动到b点的过程中,电场力将做正(选填“正”或“负”)功,质子的速度将增大(选填“增大”或“减小”)