题目内容
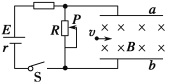
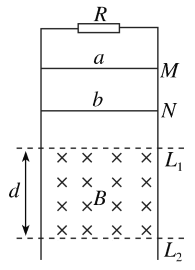
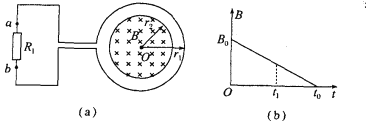
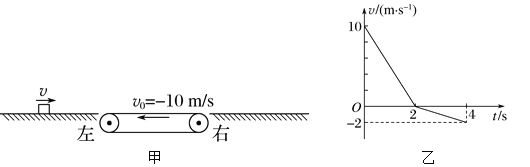
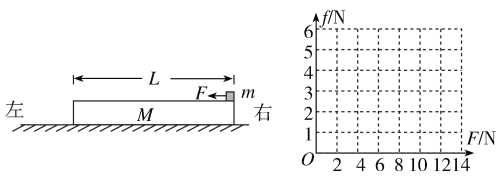
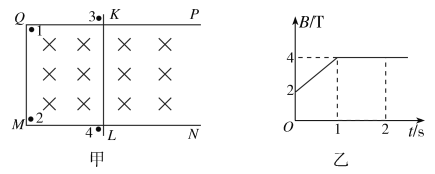
【题目】如图甲所示，不变形、足够长、质量为m1＝0.2 kg的“U”形金属导轨PQMN放在绝缘水平桌面上，QP与MN平行且距离d＝1 m，Q、M间导体电阻阻值R＝4 Ω，右内侧紧靠两固定绝缘小立柱1、2；光滑金属杆KL电阻阻值r＝1 Ω，质量m2＝0.1 kg，垂直于QP和MN，与QM平行且距离L＝0.5 m，左侧紧靠两固定绝缘小立柱3、4.金属导轨与桌面的动摩擦因数μ＝0.5，最大静摩擦力等于滑动摩擦力，其余电阻不计．从t＝0开始，垂直于导轨平面的磁场磁感应强度如图乙所示．
(1)求在整个过程中，导轨受到的静摩擦力的最大值fmax；
(2)如果从t＝2 s开始，给金属杆KL水平向右的外力，外力对金属杆作用的功率保持不变为P0＝320 W，杆到达最大速度时撤去外力，求撤去外力后QM上产生的热量QR＝？
【答案】(1)0.8 N (2)4 J
【解析】(1)在0－1 s时间内，设t时刻磁场磁感应强度为B，QKLM中的感应电动势为E，电流为I，金属导轨QM受到的安培力为F，则由乙图得B＝2＋2t(T)
由法拉第电磁感应定律，得E＝
又ΔΦ＝dLΔB
I＝
解得
＝2 T/s，E＝1 V，I＝0.2 A
导轨所受的安培力F＝BId＝(2＋2t)Id
当t＝1 s时，安培力最大为Fm，则Fm＝0.8 N
设金属导轨PQMN受到的最大静摩擦力为fm，则
fm＝μ(m1＋m2)g＝1.5 N
1 s以后，电动势为零，QM受到的安培力为零．即安培力最大时，仍然小于金属导轨PQMN受到的最大静摩擦力，金属导轨PQMN始终静止，受到的是静摩擦力
所以fmax＝Fm，则得fmax＝0.8 N
(2)从t＝2 s开始后，导轨QM受到的安培力向右，由于小立柱1、2的作用，金属导轨PQMN静止．设杆KL的最大速度为vm时，感应电动势为E1，电流为I1，受到的安培力为F1，外力为F0，则E1＝B0dvm，I1＝
则得F1＝B0I1d，有F0vm＝P0
即
＝
解得vm＝10 m/s
撤去外力直到停下来，产生的总热量为Q0，则
Q0＝
m2v
QM上产生的热量QR＝
R
代入数据，解得Q0＝5 J，QR＝4 J
