题目内容
【题目】如图所示,半径R=0.5 m的光滑圆弧面CDM分别与光滑斜面体ABC和斜面MN相切于C、M点,O为圆弧圆心,D为圆弧最低点.斜面体ABC固定在地面上,顶端B安装一定滑轮,一轻质软细绳跨过定滑轮(不计滑轮摩擦)分别连接小物块P、Q(两边细绳分别与对应斜面平行),并保持P、Q两物块静止.若PC间距为L1=0.25 m,斜面MN足够长,物块P质量m=3 kg,与MN间的动摩擦因数μ=![]() ,求:(sin37°=0.6,cos37°=0.8)
,求:(sin37°=0.6,cos37°=0.8)
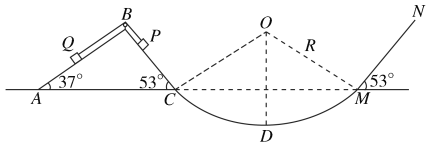
(1)烧断细绳后,物块P第一次到达D点时对轨道的压力大小;
(2)物块P第一次过M点后0.3 s到达K点,则MK间距多大;
(3)物块P在MN斜面上滑行的总路程.
【答案】(1)78 N (2)0.17 m (3)1.0 m
【解析】(1)滑块由P到D过程,由动能定理,得
mgh=![]() mv
mv![]()
根据几何关系,有h=L1sin53°+R(1-cos53°)
在D点,支持力和重力的合力提供向心力,有
FD-mg=m![]()
解得FD=78 N
由牛顿第三定律得,物块P对轨道的压力大小为78 N
(2)PM段,根据动能定理,有
mgL1sin53°=![]() mv
mv![]()
解得vM=2 m/s
沿MN向上运动过程,根据牛顿第二定律,得到
a1=gsin53°+μgcos53°=10 m/s2
根据速度时间公式,有vM=a1t1
解得t1=0.2 s
所以t1=0.2 s时,P物到达斜面MN上最高点,故返回过程,有
x=![]() a2t
a2t
沿MN向下运动过程,根据牛顿第二定律,有
a2=gsin53°-μgcos53°=6 m/s2
根据运动学公式,有xMK=![]() t1-
t1-![]() a2t=0.17 m
a2t=0.17 m
即MK之间的距离为0.17 m
(3)最后物体在CM之间来回滑动,且到达M点时速度为零,对从P到M过程运用动能定理,得到
mgL1sin53°-μmgcos53°·L总=0
解得L总=1.0 m
即物块P在MN斜面上滑行的总路程为1.0 m

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案