题目内容
【题目】如图,质量M=1 kg的木板静止在水平面上,质量m=1 kg、大小可以忽略的铁块静止在木板的右端.设最大摩擦力等于滑动摩擦力,已知木板与地面间的动摩擦因数μ1=0.1,铁块与木板之间的动摩擦因数μ2=0.4,取g=10 m/s2.现给铁块施加一个水平向左的力F.
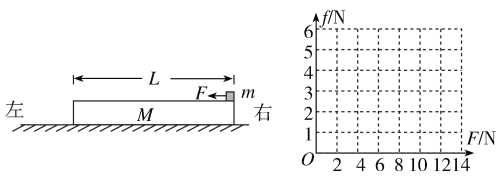
(1)若力F恒为8 N,经1 s铁块运动到木板的左端.求:木板的长度L;
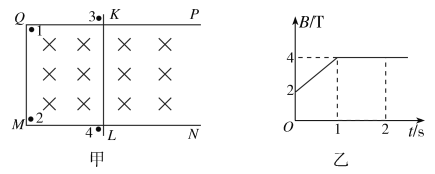
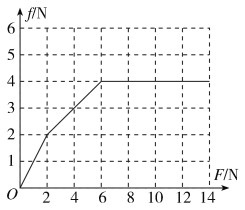
(2)若力F从零开始逐渐增加,且木板足够长.试通过分析与计算,在图中作出铁块受到的摩擦力f随力F大小变化的图像.
【答案】(1)1 m (2)f-F图像见解析
【解析】(1)铁块,由牛顿第二定律F-μ2mg=ma1①
木板,由牛顿第二定律μ2mg-μ1(M+m)g=Ma2②
设木板的长度为L,经时间t铁块运动到木板的左端,则
s木=![]() a2t2③
a2t2③
s铁=![]() a1t2④
a1t2④
又s铁-s木=L⑤
联立①②③④⑤式,解得L=1 m⑥
(2)①当F≤μ1(m+M)g=2 N时,系统没有被拉动,静摩擦力与外力成正比,
即f=F
②当F>μ1(m+M)g=2 N时,如果M、m相对静止,铁块与木板有相同的加速度a,则
F-μ1(m+M)g=(m+M)a⑦
F-f=ma⑧
解得F=2f-2⑨
此时f≤μ1mg=4 N,也即F≤6 N⑩
所以当2 N<F≤6 N时,f=+1 N
③当F>6 N时,M、m相对滑动,此时铁块受到的摩擦力为f=μ2mg=4 N
图像如图所示:

练习册系列答案
相关题目