题目内容
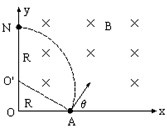
如图所示,有界匀强磁场的磁感应强度为B,区域足够大,方向垂直于纸面向里,直角坐标系xoy的y轴为磁场的左边界,A为固定在x轴上的一个放射源,内装镭核( Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿
Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿 方向飞离磁场,N点到O点的距离为L,已知OA间距离为
方向飞离磁场,N点到O点的距离为L,已知OA间距离为 L,α粒子质量为m,电荷量为q,氡核的质量为m0,
L,α粒子质量为m,电荷量为q,氡核的质量为m0,

(1)、写出镭核的衰变方程;
(2)、如果镭核衰变时释放的能量全部变为α粒子和氡核的动能,求一个原来静止的镭核衰变时放出的能量。
 Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿
Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿 方向飞离磁场,N点到O点的距离为L,已知OA间距离为
方向飞离磁场,N点到O点的距离为L,已知OA间距离为 L,α粒子质量为m,电荷量为q,氡核的质量为m0,
L,α粒子质量为m,电荷量为q,氡核的质量为m0,
(1)、写出镭核的衰变方程;
(2)、如果镭核衰变时释放的能量全部变为α粒子和氡核的动能,求一个原来静止的镭核衰变时放出的能量。
(1)、 Ra→
Ra→ Rn+
Rn+ He (2)
He (2)
 Ra→
Ra→ Rn+
Rn+ He (2)
He (2)
试题分析:(1)由质数和核电荷数守恒写核反应方程;
(2)镭核衰变放出α粒子和氡核,分别在磁场中做匀速圆周运动,根据结合关系求出α粒子在磁场中做匀速圆周运动的半径,根据半径公式求出速度,求出α粒子的动能,衰变过程中动量守恒,求出氡核反冲的动能,两者动能之和即为原来静止的镭核衰变时放出的能量.
解:(1)镭核衰变方程为:
 Ra→
Ra→ Rn+
Rn+ He
He(2)镭核衰变放出α粒子和氡核,分别在磁场中做匀速圆周运动,α粒子射出y轴时平行于x轴,设α粒子在磁场中的轨道半径为R,其圆心位置如图中O′点,
有
 ,
,则
 ,α粒子在磁场中做匀速圆周运动,有
,α粒子在磁场中做匀速圆周运动,有 ,即
,即 ,
,α粒子的动能为

∴衰变过程中动量守恒mv=m0v0,
则氡核反冲的动能为

∴

答:(1)镭核的衰变方程为 22688 Ra→ 22286 Ra+ 42 He;
(2)一个原来静止的镭核衰变时放出的能量为(5qBl)2(m+m0) 128mm0 .
点评:本题考查了核反应方程,和动量守恒定律,关键是知道谁和谁动量守恒及粒子在匀强磁场中的运动情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




 :1
:1 。求:
。求:
 ;
;
 ;
;