题目内容
如图所示,矩形区域Ⅰ和Ⅱ内分别存在方向垂直于纸面向外和向里的匀强磁场(AA′、BB′、CC′、DD′为磁场边界,四者相互平行),磁感应强度大小均为B,矩形区域的长度足够长,两磁场宽度及BB′与CC′之间的距离均相同。某种带正电的粒子从AA′上的O1处以大小不同的速度沿与O1A成α=30°角进入磁场(如图所示,不计粒子所受重力),当粒子的速度小于某一值时,粒子在区域Ⅰ内的运动时间均为t0;当速度为v0时,粒子在区域Ⅰ内的运动时间为 。求:
。求:

⑴粒子的比荷 ;
;
⑵磁场区域Ⅰ和Ⅱ的宽度d;
⑶速度为v0的粒子从O1到DD′所用的时间。
 。求:
。求:
⑴粒子的比荷
 ;
;⑵磁场区域Ⅰ和Ⅱ的宽度d;
⑶速度为v0的粒子从O1到DD′所用的时间。
(1)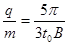 (2)
(2)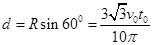 (3)t=
(3)t=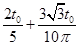
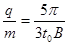 (2)
(2)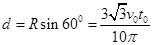 (3)t=
(3)t=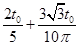
试题分析:解:(1)若速度小于某一值时粒子不能从BB′ 离开区域Ⅰ,只能从AA′边离开区域Ⅰ。则无论粒子速度大小,在区域Ⅰ中运动的时间相同。轨迹如图所示(图中只画了一个粒子的轨迹)。
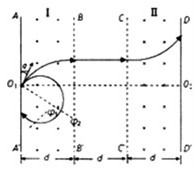
则粒子在区域Ⅰ内做圆周运动的圆心角为φ1=300o
由Bqv=

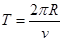
得:粒子做圆周运动的周期 T =
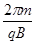
由
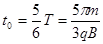
解得:
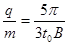
(2)速度为v0时粒子在区域I内的运动时间为
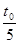 ,设轨迹所对圆心角为φ2。
,设轨迹所对圆心角为φ2。由
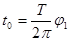
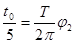
得:
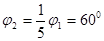
所以其圆心在BB′上,穿出BB′ 时速度方向与BB′ 垂直,其轨迹如图所示,设轨道半径为R
由
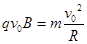 得:
得: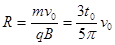
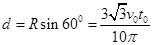
(3)区域I、Ⅱ宽度相同,则粒子在区域I、Ⅱ中运动时间均为
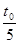
穿过中间无磁场区域的时间为t′ =
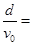
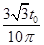
则粒子从O1到DD′所用的时间t=
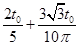
点评:带电粒子在匀强磁场中的运动是整个高中的重点,也是高考的必考的内容,粒子的运动过程的分析是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
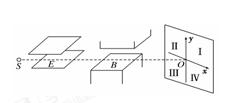

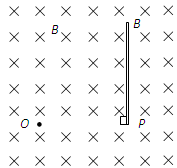
 ,则挡板至少多长,挡板吸收的粒子数占总粒子数的比值最大,并求该值。
,则挡板至少多长,挡板吸收的粒子数占总粒子数的比值最大,并求该值。 Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿
Ra)沿着与+x成θ角方向释放一个α粒子后衰变成氡核(Rn)。α粒子在y轴上的N点沿 方向飞离磁场,N点到O点的距离为L,已知OA间距离为
方向飞离磁场,N点到O点的距离为L,已知OA间距离为 L,α粒子质量为m,电荷量为q,氡核的质量为m0,
L,α粒子质量为m,电荷量为q,氡核的质量为m0,
 m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=16.3T。围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm。现将一个质量为m="0.1g" ,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知
m的圆形弹性围栏,在围栏区域内有图示方向的匀强磁场,磁感应强度大小为B=16.3T。围栏最低点一个小洞b,在b点正下方的电场区域内有一点a,a点到MN的距离d1=45cm,到PQ距离d2=5cm。现将一个质量为m="0.1g" ,带电量q=2×10-3C的带正电小球(重力不计),从a点由静止释放,在电场力作用下向下运动与挡板PQ相碰后电量减少到碰前的0.8倍,且碰撞前后瞬间小球的动能不变,不计空气阻力以及小球与围栏碰撞时的能量损失,试求:(已知 ,
, )
)
 中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为
中存在有界的匀强聚焦磁场,方向垂直坐标平面向外,磁场边界PQ直线与x轴平行,距x轴的距离为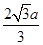 ,边界POQ的曲线方程为
,边界POQ的曲线方程为 。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求:
。且方程对称y轴,在坐标x轴上A处有一粒子源,向着不同方向射出大量质量均为m、电量均为q的带正电粒子,所有粒子的初速度大小相同均为v,粒子通过有界的匀强磁场后都会聚焦在x轴上的F点.已知A点坐标为(-a,0),F点坐标为(a,0).不计粒子所受重力和相互作用求:



