题目内容
（2）．（9分）如图所示，在光滑绝缘水 平面上有两个带电小球
、
，质量分别为3m和m，小球带正电q，小球带负电-2q，开始时两小球相距s0，小球有一个水平向右的初速度v0，小球的初速度为零，若取初始状态下两小球构成的系统的电势能为零，试证明：当两小球的速度相同时系统的电势能最大，并求出该最大值；
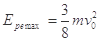
解析试题分析：（1）由于两小球构成的系统合外力为零，设某状态下两小球的速度分别为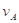
和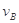
，由动量守恒定律得 
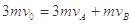（1） （2分）
所以，系统的动能减小量为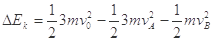 
（2） （2分）
由于系统运动过程中只有电场力做功，所以系统的动能与电势能之和守恒，考虑到系统初状态下电势能为零，故该状态下的电势能可表为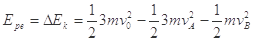
（3） （1分）
联立（1）、（3）两式，得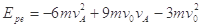 
（4）（1分）
由（4）式得：当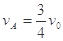 
（5） （1分）
时，系统的电势能取得最大值，而将（5）式代入（1）式，得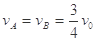 
（6）（1分）
即当两小球速度相同时系统的电势能最大，最大值为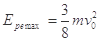 （7） （1分）
考点：动量守恒定律；能量守恒定律．
练习册系列答案
阅读快车系列答案
相关题目
暴雨前，有一云层（相当于带电体）正慢慢靠近地面，某野外地面附近有一质量较小的带电体被吸上天空，以下说法正确的是
| A．带电体在上升中电势能越来越大 |
| B．带电体在上升中跟云层间的电势差越来越大 |
| C．带电体在上升中所处环境的电场强度是越来越大 |
| D．带电体的加速度越来越大 |
，此区域外导轨是光滑的。电动小车沿PS以v=1.0m/s的速度匀速前进时，滑杆经d=1m的位移由AA’滑到OO’位置。（g取10m/s2）求：
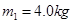的平板小车，小车的右端有一固定的竖直挡板，挡板上固定一轻质细弹簧．位于小车上A点处的质量为
的木块(视为质点)与弹簧的左端相接触但不连接，此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间有摩擦，与A点右侧的车面之间的摩擦可忽略不计．现小车与木块一起以
的初速度向右运动，小车将与其右侧的竖直墙壁发生碰撞，已知碰撞时间极短，碰撞后小车以
的速度水平向左运动，取
．
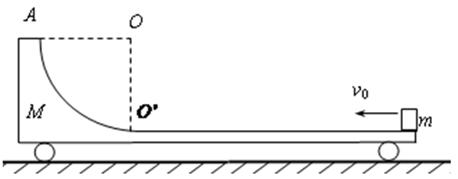
点相切．现将一质量m =" 1.0" kg的小物块（可视为质点）从平板车的右端以水平向左的初速度v0滑上平板车，小物块与水平轨道间的动摩擦因数
，小物块恰能到达圆弧轨道的最高点A．取g =" 10" m/s2，求：
