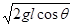题目内容
(10分)如图所示，在光滑水平地面上，有一质量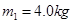
的平板小车，小车的右端有一固定的竖直挡板，挡板上固定一轻质细弹簧．位于小车上A点处的质量为
的木块(视为质点)与弹簧的左端相接触但不连接，此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间有摩擦，与A点右侧的车面之间的摩擦可忽略不计．现小车与木块一起以
的初速度向右运动，小车将与其右侧的竖直墙壁发生碰撞，已知碰撞时间极短，碰撞后小车以
的速度水平向左运动，取
．
(i)求小车与竖直墙壁发生碰撞的过程中小车动量变化量的大小；
(ii)若弹簧始终处于弹性限度内，求小车撞墙后与木块相对静止时的速度大小和弹簧的最大弹性势能；
（1）
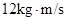（2）v = 0.40m/s EP＝3.6 J
解析试题分析：（ⅰ）以v1的方向为正方向，则小车与竖直墙壁发生碰撞的过程中，小车动量变化量的大小为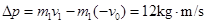 
①
（ⅱ）小车与墙壁碰撞后向左运动，木块与小车间发生相对运动将弹簧压缩至最短时，二者速度大小相等，此后木块和小车在弹簧弹力和摩擦力的作用下，做变速运动，直到二者再次具有相同速度，此后，二者相对静止。整个过程中，小车和木块组成的系统动量守恒
设小车和木块相对静止时的速度大小为v，根据动量守恒定律有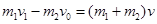
②
解得 v =" 0.40m/s" ③
当小车与木块首次达到共同速度v时，弹簧压缩至最短，此时弹簧的弹性势能最大
设最大弹性势能为EP，根据机械能守恒定律可得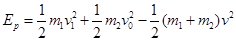 
④
EP＝3.6 J ⑤
评分参考：第(1)问2分；第(ⅱ)问8分，其中②式3分，③式1分，④式3分，⑤式1分。
考点：动量守恒定律 功能关系
质量为1.0 kg的小铁球从某一高度自由落下，当下落到全程中点位置时，具有36 J的动能，如果空气阻力不计，取地面为零势能面，g取10 m/s2，则下列说法正确的是
| A．铁球在最高点时的重力势能为36 J |
| B．铁球在全程中点位置时具有72 J机械能 |
| C．铁球落到地面时速度大小为12 m/s |
| D．铁球开始下落时的高度为7.2 m |
、
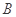，质量分别为3m和m，小球
C的点电荷所受电场力的大小
N。求：
