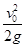如图所示.光滑水平面上有一质量M = 4.0 kg的带有圆弧轨道的平板车.车的上表面是一段长L=1.5m的粗糙水平轨道.水平轨道左侧连一半径R = 0.25 m 的四分之一光滑圆弧轨道.圆弧轨道与水平轨道在点相切．现将一质量m = 1.0 kg的小物块从平板车的右端以水平向左的初速度v0滑上平板车.小物块与水平轨道间的动摩擦因数.小物块恰能到达圆弧轨道的� 题目和参考答案——青夏教育精英家教网—

题目内容

(9分)如图所示，光滑水平面上有一质量M =" 4.0" kg的带有圆弧轨道的平板车，车的上表面是一段长L=1.5m的粗糙水平轨道，水平轨道左侧连一半径R =" 0.25" m 的四分之一光滑圆弧轨道，圆弧轨道与水平轨道在点相切．现将一质量m =" 1.0" kg的小物块（可视为质点）从平板车的右端以水平向左的初速度v₀滑上平板车，小物块与水平轨道间的动摩擦因数，小物块恰能到达圆弧轨道的最高点A．取g =" 10" m/s²，求：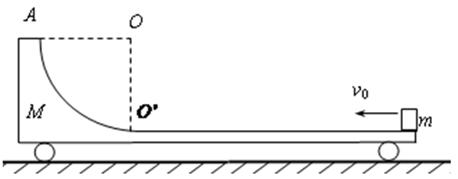

（1）小物块滑上平板车的初速度v₀的大小．
（2）小物块与车最终相对静止时，它距点的距离．

（1）（2）

解析试题分析：（1）平板车和小物块组成的系统水平方向动量守恒，设小物块到达圆弧最高点A时，二者的共同速度
由动量守恒得：         ①        (2分)
由能量守恒得：       ②           (2分)
联立①②并代入数据解得：　　    ③         (1分)
（2）设小物块最终与车相对静止时，二者的共同速度v₂，从小物块滑上平板车，到二者相对静止的过程中，由动量守恒得： ④       (1分)
设小物块与车最终相对静止时，它距O′点的距离为x。由能量守恒得：
   ⑤          (2分)
联立③④⑤并代入数据解得：     　⑥         (1分)
考点：动量守恒  功能关系

练习册系列答案

相关题目

如下图所示，质量为M、长度为l的小车静止在光滑的水平面上．质量为m的小物块(可视为质点)放在小车的最左端．现用一水平恒力F作用在小物块上，使小物块从静止开始做匀加速直线运动．小物块和小车之间的摩擦力为Ff，小物块滑到小车的最右端时，小车运动的距离为x，在这个过程中，以下结论正确的是(　　)

A．小物块到达小车最右端时具有的动能为F(l＋x)

B．小物块到达小车最右端时，小车具有的动能为Ffx

C．小物块克服摩擦力所做的功为Ffl

D．小物块和小车增加的机械能为Fx

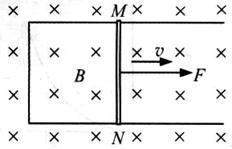
（20）导体切割磁感线的运动可以从宏观和微观两个角度来认识。如图所示，固定于水平面的U形导线框处于竖直向下的匀强磁场中，金属直导线MN在与其垂直的水平恒力F的作用下，在导线框上以速度v做匀速运动，速度v与恒力F方向相同，导线MN始终与导线框形成闭合电路，已知导线MN电阻为R，其长度L，恰好等于平行轨道间距，磁场的磁感应强度为B，忽略摩擦阻力和导线框的电阻。

（1）通过公式推导验证：在时间内，F对导线MN所做的功W等于电路获得的电能，也等于导线MN中产生的焦耳热Q。
（2）若导线的质量m=8.0g，长度L=0.1m，感应电流I=1.0A，假设一个原子贡献1个自由电子，计算导线MN中电子沿导线长度方向定向移动的平均速率v（下表中列出了一些你可能用到的数据）。

（3）经典物理学认为，金属的电阻源于定向运动自由电子和金属离子（金属原子失去电子后剩余部分）的碰撞，展开你想象的翅膀，给出一个合理的自由电子运动模型：在此基础上，求出导线MN中金属离子对一个自由电子沿导线长度方向的平均作用力的表达式。

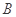（2）．（9分）如图所示，在光滑绝缘水平面上有两个带电小球、，质量分别为3m和m，小球带正电q，小球带负电-2q，开始时两小球相距s₀，小球有一个水平向右的初速度v₀，小球的初速度为零，若取初始状态下两小球构成的系统的电势能为零，试证明：当两小球的速度相同时系统的电势能最大，并求出该最大值；

(10分) 图示为一匀强电场，已知场强E=2×10²N/C。现让一个电量q=4×10^-8C的电荷沿电场方向从M点移到N点，MN间的距离s=30cm。试求：

（1）电荷从M点移到N点电势能的变化；
（2）M、N两点间的电势差。

（本题8分）.如图所示，为一传送装置，其中AB段粗糙，AB段长为L＝0.2 m，动摩擦因数μ＝0.6，BC、DEN段均可视为光滑，且BC的始、末端均水平，具有h＝0.1 m的高度差，DEN是半径为r＝0.4 m的半圆形轨道，其直径DN沿竖直方向，C位于DN竖直线上，CD间的距离恰能让小球自由通过．在左端竖直墙上固定一轻质弹簧，现有一可视为质点的小球，小球质量m＝0.2 kg，压缩轻质弹簧至A点后由静止释放(小球和弹簧不粘连)，小球刚好能沿DEN轨道滑下．求：

(1)小球到达N点时的速度；
(2)压缩的弹簧所具有的弹性势能。

如图所示，一小物块自平台上以速度水平抛出，刚好落在邻近一倾角为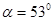的粗糙斜面顶端，并恰好沿该斜面下滑，已知斜面顶端与平台的高度差m，小物块与斜面间的动摩擦因数为，点离点所在平面的高度m。有一半径为R的光滑圆轨道与斜面AB在B点平滑连接，已知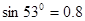，，取m/s²。求：

（1）小物块水平抛出的初速度是多少；
（2）小物块能够通过圆轨道，圆轨道半径R的最大值。

（10分）如图所示，将质量均为m厚度不计的两物块A、B用轻质弹簧相连接．第一次只用手托着B物块于H高处，A在弹簧弹力的作用下处于静止，现将弹簧锁定，此时弹簧的弹性势能为，现由静止释放A、B，B物块着地后速度立即变为0，同时弹簧锁定解除，在随后的过程中B物块恰能离开地面但不继续上升．第二次用手拿着A、B两物块，使得弹簧竖直并处于原长状态，此时物块B离地面的距离也为H，然后由静止同时释放A、B，B物块着地后速度同样立即变为0．求：

（1）第二次释放A、B后，A上升至弹簧恢复原长时的速度；
（2）第二次释放A、B后，B刚要离地时A的速度．

如图所示，在小车的支架上用细线悬挂一个小球，已知线长为L，小车带着小球一起以速度向右做匀速运动。当小车突然碰到障碍物而停止运动后，关于小球再上升的最大高度h的下列几种表述中，肯定不可能的是（）

试题分类