题目内容
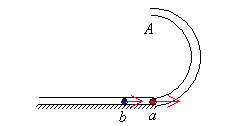
如图9所示，半径为R，内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点A时，对管壁上部的压力为3mg，b通过最高点A时，对管壁下部的压力为0.75mg，求a、b两球落地点间的距离。
s=3R
在最高点C时对管壁上部的压力为3mg，根据牛顿第三定律，管壁对A向下的压力为3mg，由于在C时处于圆周运动的最高点，所以合外力提供向心力
mg+3mg=mvA2/R ( 2分 )
vA=
A离开C做平抛运动，下降2R落地 落地时间t
2R=gt2/2 ( 2分 )
Sa=VAt
可得Sa="4R" ( 2分 )
同理B通过最高点C时，对管壁的下端的压力为0.75mg,根据牛顿第三定律，管壁对B向上的支持力0.75mg
mg-0.75mg=mvB2/R
vB=
SB= vB t
可得SB="R" ( 2分 )
所以A、B两球落地点间的距离
s=Sa-SB=4R-R=3R ( 2分 )
mg+3mg=mvA2/R ( 2分 )
vA=
A离开C做平抛运动，下降2R落地 落地时间t
2R=gt2/2 ( 2分 )
Sa=VAt
可得Sa="4R" ( 2分 )
同理B通过最高点C时，对管壁的下端的压力为0.75mg,根据牛顿第三定律，管壁对B向上的支持力0.75mg
mg-0.75mg=mvB2/R
vB=
SB= vB t
可得SB="R" ( 2分 )
所以A、B两球落地点间的距离
s=Sa-SB=4R-R=3R ( 2分 )
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
kg的汽车以不变的速度先后驶过凹形桥面和凸形桥面，两桥面的圆弧半径均为20m。由于轮胎太旧，如果受到超过3×
N的压力时就会出现爆胎，则：
.
圆形轨道，位于竖直平面内，轨道半径为R， 下端与水平绝缘轨道在B点平滑连接，整个轨道处在水平向左的匀强电场中． 现有一质量为m、带正电的小滑块（可视为质点）置于水平轨道上，滑块受到的电场力大小为
，滑块与水平轨道间的动摩擦因数为0.5，重力加速度为g．