题目内容
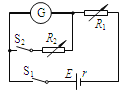
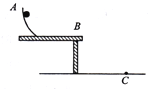
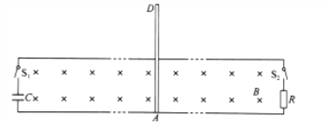
【题目】水平面内有两根足够长的平行光滑金属导轨，间距为L，两端分别通过开关接有电容为C的电容器和阻值为R的电阻，导轨间有垂直导轨平面向里的勾强磁场，磁感应强度大小为B。一质量为m，长为2L的金属棒AD与导轨垂直放置，A端恰好与导轨接触，初始状态如图所示。开始时开关S1、S2均断开，除电阻R外，其他电阻均不计，金属棒始终与导轨接触良好。
(1)只闭合开关S1，让金属棒以初速度
水平向右运动，求金属棒的最終速度大小。
(2)闭合开关S1、S2，让金属棒绕A端以角速度ω匀速转过90°的过程中，求通过电阻R的电荷量。
(3)只闭合开关S2，让金属棒以初速度水平向右运动，求它运动的速度大小随位移x的变化关系。
【答案】（1）
（2）
（3） 
【解析】
（1）最终电容器两极板间的电压等于导体棒产生的感应电动势，即
，
又知道
，
对金属棒由动量定理可得
，而
联立解得
（2）金属棒转过60°过程中，由法拉第电磁感应定律可得
平均感应电流
通过R的电荷量
金属棒转过60°时的电动势
此时电容器所答的电荷量为
金属棒转过60°后，电容器迅速放电，通过R上的电荷量
，
金属棒转过90°的过程中，通过电阻R的上电荷量：
（3）金属棒运动的过程中受到为v时，感应电动势
感应电流
导体棒所受安培力
根据动量定理
，即
，
联立解得
对连续变化过程，方程两边累加可解得
，（
）
练习册系列答案
相关题目
