题目内容
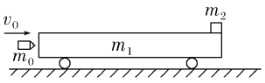
【题目】如图所示,一质量![]() kg的平顶小车静止在光滑的水平轨道上。质量
kg的平顶小车静止在光滑的水平轨道上。质量![]() kg的小物块(可视为质点)静止在车顶的右端。一质量为m0=0.05kg的子弹以水平速度
kg的小物块(可视为质点)静止在车顶的右端。一质量为m0=0.05kg的子弹以水平速度![]() 射中小车左端并留在车中,最终小物块相对地面以v=2m/s的速度滑离小车。已知子弹与小车的作用时间极短,小物块与车顶面的动摩擦因数
射中小车左端并留在车中,最终小物块相对地面以v=2m/s的速度滑离小车。已知子弹与小车的作用时间极短,小物块与车顶面的动摩擦因数![]() ,认为最大静摩擦力等于滑动摩擦力。取g=10m/s2,求:
,认为最大静摩擦力等于滑动摩擦力。取g=10m/s2,求:
(1)子弹相对小车静止时小车速度的大小v1;
(2)物块在小车上滑行的时间t;
(3)求物块离开小车时小车的速度v2和小车的长度L。
【答案】(1)10m/s;(2)0. 25s;(3)![]() ,2m
,2m
【解析】
(1)子弹进入小车的过程中,子弹与小车组成的系统动量守恒,由动量守恒定律得
![]()
解得
![]() 。
。
(2)对物块,根据动量定理:
![]()
解得
t=0. 25s
(3)三物体组成的系统动量守恒,由动量守恒定律得
![]()
解得
![]()
由能量守恒可得
![]()
解得
L=2m

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
【题目】某物理兴趣小组在“探究弹性势能的表达式”的实验中,用一个被压缩的弹簧沿粗糙水平面弹出一个小物体,测得弹簧被压缩的距离![]() 和小物体在粗糙水平面上滑动的距离
和小物体在粗糙水平面上滑动的距离![]() 如下表所示。
如下表所示。
实验次数 | 1 | 2 | 3 | 4 |
d/cm | 1.00 | 2.00 | 3.00 | 4.00 |
x/m | 1.00 | 4.02 | 9.01 | 16.02 |
(1)由此表可以归纳出,小物体滑动的距离![]() 与弹簧被压缩的距离
与弹簧被压缩的距离![]() 之间的关系为x=___(式中的常量用
之间的关系为x=___(式中的常量用![]() 表示)。
表示)。
(2)弹簧的弹性势能![]() 与弹簧被压缩的距离
与弹簧被压缩的距离![]() 之间的关系为
之间的关系为![]() =____ (式中的常量用k2表示)。
=____ (式中的常量用k2表示)。